
ARITMÉTICA
IFSP - Cursinho Popular
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
Introdução
Tópicos: Razão, Grandezas, grandezas diretamente proporcionais, grandezas inversamente proporcionais, razões entre grandezas de mesma natureza, razões entre grandezas de natureza distintas, porcentagem, proporção, propriedade fundamental das proporções, regra de três simples e regra de três composta.
Contextualização: Os tópicos da aritmética são utilizados desde os princípios da civilização humana, relacionando as grandezas e suas relações entre si. Tendo diversas aplicações em vários ramos do conhecimento.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Razão
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
Figura 1 – Avião Airbus A380.

Fonte: Pixabay (2015) (https://pixabay.com/)
O avião revolucionou a forma como a humanidade pode se deslocar ao redor do mundo inteiro, de um continente ao outro, em horas, no máximo, um dia. Do 14-Bis inventado por Santos Dumont (em 1906), chegamos (atualmente) ao Airbus A380 com capacidade padrão de 489 a 615 passageiros distribuídos em 72,72 metros de comprimento. Da ponta de uma asa até a outra, lá se vão 79,75 metros de envergadura. Com 24,09 metros de altura (relativo a um prédio de 7 andares) esta aeronave é o maior avião comercial já construído na história.
Diante destas dimensões podemos fazer algumas considerações interessantes. Na configuração para 489 passageiros, estamos distribuindo, aproximadamente 6,7 pessoas por cada metro do seu comprimento. Ao passo, que se colocarmos 615 passageiros, a razão sobe para 8,45 pessoas por metro.
Note que nesta última frase usamos o termo razão para nos referirmos à comparação entre a quantidade de passageiros e o comprimento do avião. Esta forma de fazer comparação entre valores (medidas) é bem conhecida no universo da matemática e muito simples de ser determinada. Veja!
No caso acima estamos comparando total de passageiros com comprimento do avião, assim, a razão entre esses valores é dada por:
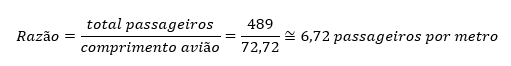
Assim, podemos definir a Razão entre dois números como a divisão ou o quociente entre eles, sendo que o número divisor deve ser necessariamente diferente de zero (já que não existe divisão por zero). Reescrevendo isso numa linguagem algébrica temos:
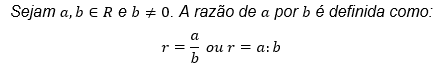
e lemos a expressão "a está para b" ou "a para b".

O que acha de praticar para ver se entendeu?
1- Considere uma classe com 40 alunos, sendo 25 meninos e 15 meninas,
a) Qual é a razão do número de meninas pelo número de meninos?
b) Qual é a razão do número de meninos pelo número de meninas?
c) Qual é a razão do número de meninas pelo número de alunos?
d) Qual é a razão do número de meninos pelo número de alunos?
(Simplifique as frações)
2- A razão entre a idade de um marido e sua esposa é 9/8. Sabendo que a idade da esposa é de 40 anos, qual é a idade do marido?
Agora que você já praticou, vamos ver o porquê a Razão é tão conhecida no universo da matemática.
Taxa percentual
A taxa percentual t consiste na razão r de dois números comparados com cem, ou ainda,

Logo, a taxa percentual é.

EXEMPLO
Figura 2 – Televisão.

Fonte: Pixabay (2018), (https://pixabay.com/)
Para resolvermos tal exemplo faremos a diferença do valor habitual (R$1.500,00) pelo valor na promoção (R$1.000,00) e então obtermos o valor do desconto.
R$1.500,00 - R$1.000,00 = R$500,00
Agora precisamos fazer a razão entre o valor do desconto (R$500,00) pelo valor habitual (R$1.500,00) e multiplicar por 100, para obtermos a taxa percentual de desconto.![]()
Portanto, chegamos à conclusão de que a taxa percentual de desconto do televisor é aproximadamente 33,33%.
Probabilidade
Figura 3 – dado.
Fonte: Pixabay (2017) (https://pixabay.com/)
Este conceito matemático indica a chance de que determinado evento ocorra em contraposição as demais possibilidades de eventos distintos poderem ocorrer. Consiste na razão entre o número de possibilidades de que determinado evento ocorra, pelo número total de possibilidades de todos os eventos possíveis.
Por exemplo, ao lançar um dado existem um total de 6 possibilidades distintas de valores que podem estar sob a face superior após o lançamento. Uma dessas possibilidades resulta o valor 1, as outras 5 possibilidades são os valores 2,3,4,5 e 6. Portanto, a probabilidade de lançar um dado e cair o número um é:
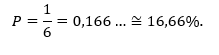
Assim, ao jogar um dado, qual seria a probabilidade de cair o número:
- 1 ou 2?
- 1,2 ou 3?
- 1,2,3 ou 4?
A resposta seria:
(a) Se 1 e 2 são dois valores dentre os 6 possíveis, a chance é de 2 para 6, isto é,
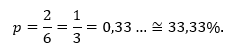
(b) Para que caia 1,2 ou 3, estamos falando de três valores entre os seis possíveis, logo:
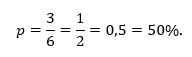
(c) Para que caia 1,2,3 ou 4, são quatro valores entre os seis possíveis, resultando em:
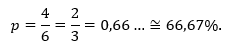
Agora é a sua vez!
EXERCÍCIOS
3- Passe as seguintes razões em notação decimal e percentual.
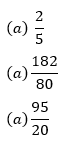
4- (ENEM 2016) Cinco marcas de pão integral apresentam as seguintes concentrações em fibras (massa de fibra por pão):
- Marca A: 2 g de fibras a cada 50 g de pão;
- Marca B: 5 g de fibras a cada 40 g de pão;
- Marca C: 5 g de fibras a cada 100 g de pão;
- Marca D: 6 g de fibras a cada 90 g de pão;
- Marca E: 7 g de fibras a cada 70 g de pão;
Recomenda-se a ingestão do pão que possui a maior concentração de fibras.
Disponível em: www.blog.saude.gov.br. Acesso em: 25 fev. 2013.
A marca a ser escolhida é
(A) A
(B) B
(C) C
(D) D
(E) E
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Grandezas
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
As grandezas são valores que podem ser medidos ou contados, podendo assumir diferentes manifestações.
Figura 4 – Fita métrica.

Fonte: Pixabay (2016) (https://pixabay.com/)
Figura 5 – Balança.

Fonte: Pixabay (2017) (https://pixabay.com/)
Figura 6 – Relógio.

Fonte: Pixabay (2015) (https://pixabay.com/)
Grandezas da informática → Bit, Byte, kilobyte, gigabyte, etc.
Figura 7 – Representação de um Algoritmo.

Fonte: Pixabay (2015) (https://pixabay.com/)
Figura 8 – Ilustração dos números binários.

Fonte: Pixabay (2017) (https://pixabay.com/)
Grandezas econômicas → produção, valor, PIB (produto interno bruto), renda per capita, etc.
Figura 9 – Representação de uma tabela de valores.

Fonte: Pixabay (2017) (https://pixabay.com/)
Grandezas físicas → massa, deslocamento, energia, volume, comprimento, área, tempo, corrente elétrica, etc.
Figura 10 – Velocímetro.

Fonte: Pixabay (2011) (https://pixabay.com/)
Figura 11 – Amperímetro.

Fonte: Pixabay (2017) (https://pixabay.com/)
Figura 12 – Medidor de Pressão Arterial.
Fonte: Pixabay (2015) (https://pixabay.com/)
Figura 13 – Termômetro.

Fonte: Pixabay (2018) (https://pixabay.com/)
Grandezas químicas → massa atômica, massa molecular, massa molar, volume, etc.
Figura 14 – Instrumentos de laboratório.

Fonte: Pixabay (2013) (https://pixabay.com/)
Figura 15 – Peças representando os elementos da tabela periódica.

Fonte: Pixabay (2019) (https://pixabay.com/)
As grandezas geralmente possuem unidades de medida, a qual distingue as grandezas dimensionais umas das outras, a unidade de medida acompanha um valor numérico que quantifica a grandeza dimensional.
Exemplos: 90 km/h, 3 kg, 2 L.
Grandezas vetoriais
As grandezas vetoriais precisam de uma direção e sentido para que possam fazer sentido, como exemplo a velocidade (Figura 16 – Carro de corrida e uma representação do vetor velocidade.

Fonte: Pixabay (2016) (https://pixabay.com/)
Figura 17 – Representação do vetor força.

Fonte: Pixabay (2017) (https://pixabay.com/)
Figura 18 – Representação do vetor peso, força de arrasto e aceleração da gravidade.

Fonte: Pixabay (2017) (https://pixabay.com/)
Figura 19 – Representação do campo eletromagnético.
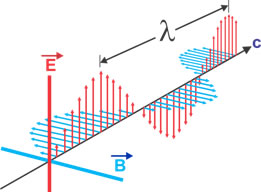
Fonte: Pixabay (2016) (https://pixabay.com/)
Grandezas escalares
As grandezas escalares não dependem da direção e do sentido, geralmente são constantes em determinadas porções do espaço, como exemplos temos as diferentes formas de energia (E), massa (m), pressão (p), temperatura (T), tempo (t), comprimento (x), área (A), etc.
Figura 20 – Aerogerador.

Fonte: Pixabay (2016) (https://pixabay.com/)
Figura 21 – Usina Hidrelétrica.

Fonte: Pixabay (2015) (https://pixabay.com/)
Figura 22 – Usina Nuclear.

Fonte: Pixabay (2017) (https://pixabay.com/)
Figura 23 – Ampulheta.

Grandezas adimensionais
As grandezas adimensionais não possuem unidade de medida, apenas um número constante. Geralmente são resultados de uma razão entre grandezas de mesma natureza, tópico no qual entraremos mais adiante. Como exemplos o índice de refração, coeficiente de elasticidade, etc.
Grandezas diretamente proporcionais
Figura 24 – Indústria de sapatos.

Fonte: Pixabay (2014) (https://pixabay.com/)
Uma indústria de sapatos possui demandas bem variadas conforme a época do ano, e então seus administradores resolvem fazer uma tabela que relaciona o número de funcionários com a quantidade de sapatos produzidos. Observe a tabela de números de funcionários em relação ao número de sapatos produzidos por dia nesta indústria. Consideremos que todos os funcionários possuem uma mesma produtividade.
Número de funcionários |
Quantidade de sapatos produzidos |
10 |
50 |
20 |
100 |
30 |
150 |
40 |
200 |
Podemos observar na tabela, que o aumento do número de funcionários acarreta um aumento proporcional na produção de sapatos. Ao dividirmos o número de funcionários da primeira linha pelo número de funcionários da segundo linha, obteremos o mesmo resultado que se dividirmos a quantidade de sapatos da primeira linha pela segunda. Como é apresentado a seguir:
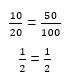
Essa propriedade pode ser generalizada em qualquer relação que façamos. Poderíamos ter analisado a 4ª e 2ª linhas, o que corresponderia ao seguinte:
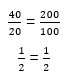
Podemos então concluir que a razão que modela a proporcionalidade entre o número de funcionários e a quantidade de sapatos produzidos é igual a ![]()
Grandezas diretamente proporcionais são grandezas que possuem uma dependência entre si, quando aumentamos uma grandeza aumentamos a outra grandeza dependente em uma proporção constante. De forma que se calcularmos a razão das grandezas, em intervalos de variação equivalentes, obteremos um mesmo resultado.
Escrevemos o sinal de proporcionalidade com a letra grega Alfa ![]() O valor A sendo diretamente proporcional a um valor B, fica da seguinte forma:
O valor A sendo diretamente proporcional a um valor B, fica da seguinte forma:

Grandezas inversamente proporcionais
Figura 25 – Cadernos.

Fonte: Pixabay (2015) (https://pixabay.com/)
Em uma indústria de cadernos são utilizadas diferentes quantidades de máquinas produtoras conforme a demanda, a tabela a seguir relaciona o número de máquinas produtoras com o número de dias necessários para a produção dos cadernos.
Número de máquinas |
Número de dias |
10 |
50 |
20 |
25 |
40 |
12,5 |
50 |
10 |
Se dividirmos o valor da primeira linha pela segunda linha, para ambas as colunas observaremos que serão valores inversos, ou seja são razões inversas. Como apresentado a seguir:
Para a primeira coluna (número de máquinas), obtemos a seguinte relação.
![]()
Para a segunda coluna (número de dias), obtemos a seguinte relação.
![]()

As razões inversas apresentam uma propriedade importante, a multiplicação entre a razão inversa e sua razão original é equivalente a um. Apliquemos tal propriedade no exemplo anterior.
![]()
As grandezas inversamente proporcionais possuem uma dependência entre si, sendo que conforme aumentamos uma grandeza diminuímos a outra grandeza, e vice-versa, de maneira proporcional, se aumentamos uma grandeza duas vezes, diminuiremos a outra pela metade e assim sucessivamente.
Escrevemos o sinal de proporcionalidade com a letra grega Alfa igual ao caso de ser diretamente proporcional. O valor A sendo inversamente proporcional a um valor B. Será expresso da seguinte forma:
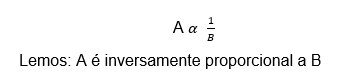
EXERCÍCIO:
5. (ENEM 2016) Para a construção de isolamento acústico numa parede cuja área mede 9 m², sabe-se que, se a fonte sonora estiver a 3 m do plano da parede, o custo é de R$ 500,00. Nesse tipo de isolamento, a espessura do material que reveste a parede é inversamente proporcional ao quadrado da distância até a fonte sonora, e o custo é diretamente proporcional ao volume do material do revestimento. Uma expressão que fornece o custo para revestir uma parede de área A (em metro quadrado), situada a D metros da fonte sonora, é...
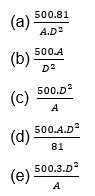
RAZÕES ENTRE GRANDEZAS DE MESMA NATUREZA
As razões entre grandezas de mesma natureza consistem, nas razões entre os números que expressam as medidas, sendo necessário de que estas medidas estejam na mesma unidade.
Tais razões dão origem a boa parte das grandezas adimensionais da física e da química.
Exemplo:
Ao comprar um achocolatado, você observa que uma marca A está R$10,00 e outra marca B está R$15,00. Sabe-se que ambas as marcas vendem o achocolato com 300 gramas.
Quantas vezes o achocolatado da marca B é mais caro comparado à marca A?
Para resolvermos utilizaremos o conceito de razão
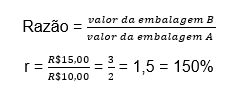
Isso quer dizer que a marca B é 1,5 vezes mais cara que a marca A. Ou que o valor da marcar B representa 150% de um total de 100% do valor da marca A ou também podemos falar que a marca B é 50% mais cara que a marca A.
Exercício
¨6. Calcule as razões entre.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Razões entre comprimentos
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
Considere os quadrados 1 e 2 com lados de 3 e 6 metros respectivamente, com as áreas 9m2 e 36m2.
Figura 27 – Quadrado 1 e quadrado 2.
Imagem do Autor
-
Qual a razão entre a área do quadrado 2 e a área do quadrado1?
-
Qual a razão entre a área do quadrado 1 e o quadrado2?
-
Qual a razão entre o lado do quadrado 2 e o lado do quadrado 1?
-
Qual a razão entre o lado do quadrado 1 e o lado do quadrado 2?
Resolução:
-
= 4, Portanto o quadrado 2 possui uma área 4 vezes maior que a área do quadrado 1.
-
=
, Portanto o quadrado 1 possui
da área do quadrado 2.
-
= 2, Podemos concluir que o comprimento da aresta do quadrado 2 é 2 vezes maior que o comprimento da aresta do quadrado 1.
-
=
, isso nos informa que o comprimento da aresta do quadrado 1 é metade do comprimento da aresta do quadrado 2.
Razões entre volumes
Considere os seguintes cubos 1 e 2 com arestas de 2 e 4 metros, e volumes de 8 e 64 metros cúbicos, respectivamente.
Figura 28 – Cubo de aresta igual a dois metros.
Imagem do Autor
Figura 29 - Cubo de aresta igual a quatro metros.
Imagem do Autor
-
Qual é a razão entre o volume do cubo2 e do cubo1?
-
Qual é a razão entre a aresta do cubo2 e do cubo1?
-
Qual é a razão entre a área das faces do cubo2 e do cubo1?
Respostas
-
= 8, Podemos concluir que o volume do cubo2 é oito vezes maior que o volume do cubo1.
-
= 2, podemos notar que a aresta do cubo2 é duas vezes maior que a aresta do cubo1.
-
= 4, podemos notar que área de cada face do cubo2 é quatro vezes maior que a área de cada face do cubo1.
É importante que notemos quando a razão entre os comprimentos da aresta for dois, a razão entre as áreas das faces será quatro (dois elevado ao quadrado), e a razão entre os volumes será oito (dois elevado ao cubo). Tal propriedade vale para qualquer razão entres cubos.
Escala
Figura 30 – Mapa.
Fonte: Pixabay (2014) (https://pixabay.com/)
Considere um mapa, onde duas cidades A e B possuem uma distância de 5 cm no mapa, e de 10.000 km na realidade. Qual é a escala do mapa?
Para relacionarmos a distância das duas cidades no mapa e na realidade, iremos calcular uma razão entre tais distâncias, e então obteremos a escala do mapa.
A razão fica da seguinte forma:
Sendo a distância no mapa igual a 5 cm, e a distância real de 10.000 km.
(I)
Para realizarmos os cálculos, as unidades de medidas devem ser as mesmas no numerador e denominador.
Podemos passar tanto 5 cm para unidade em km, quanto podemos passar 10.000 km em unidade de cm. Neste exemplo iremos passar 10.000 km em unidade de cm.
Primeiro, passamos 10.000 km para notação em potência de 10 para facilitar os cálculos.
10.000 km = 104 km
O símbolo quilo (k) equivale a 103. Então obtemos:
104 km = 104 103m = 107m
Agora que já "retiramos" o símbolo quilo (k) iremos "inserir" o símbolo centi (c). Para isso multiplicaremos por 10-2 e 102 para manter a igualdade.
107m = 107 102
10-2m
Como c equivale a 10-2.
107 102 cm = 109 cm
Então chegamos à conclusão de que 10.000 km equivalem a 109 cm. E então podemos substituir na equação (I).
Dividimos o numerador e denominador da razão por 5, e então obteremos:
= 1 : 200.000.000
E então chegamos à conclusão de que cada 1 cm no mapa equivale a 200.000.000 cm na realidade.
A escala é a razão entre o comprimento de uma representação, pelo comprimento real, estando ambos os comprimentos medidos na mesma unidade de medida. Podemos resumir essa razão na seguinte fórmula:
e = Cd/Cr
Onde,
e: escala
Cd: Comprimento do desenho (representação)
Cr: Comprimento real
EXERCÍCIOS
7. A distância entre duas cidades em trajetória retilínea equivale a 800 km, em um mapa a distância entre as cidades é de 8 cm. Qual é a escala utilizada no mapa?
8. O comprimento de um quarto em uma planta de casa é de 36 centímetros, sabendo se que o comprimento real deste mesmo quarto é de 6 metros. Qual é a escala utilizada?
9. Em uma planta de casa, foi utilizado uma escala . (a) Qual foi o comprimento real da cozinha, sendo que na planta estava com 4 cm de comprimento (b) O comprimento real do banheiro é de 3 metros, qual comprimento é observado na planta?
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Razões entre grandezas de naturezas distintas
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
As razões entre grandezas distintas possuem diversas aplicações na física, química, ciências humanas, e ciências econômicas, etc. Apresentarei algumas de suas aplicações.
APLICAÇÕES
Gramatura de papel
Consiste na razão entre a massa de papel pela sua respectiva área:
Gramatura =
Ou, de maneira resumida:
Gr = Mp/Ap
Densidade demográfica
A densidade demográfica é a razão do número de habitantes pela área que os mesmos ocupam. Podendo ser expressa da seguinte maneira:
Densidade demográfica =
Ou, de maneira resumida:
Dd = Nh/A
EXERCÍCIOS
10. Um carro percorre um espaço de 120 km em 1 hora e 30 minutos, qual foi sua velocidade média? Apresente a resposta em unidades de km/h.
11. Para medir a velocidade média de um carro de corrida, é medido o tempo que o veículo leva para percorrer um espaço de 1 km em linha reta. Considere que tenha levado 15 segundos para o automóvel percorrer o trajeto. Qual foi sua velocidade média em unidades de km/h?
12. Um ano luz é a distância que a luz percorre em um ano. Qual a distância em km de dois anos-luz? Dado: velocidade da luz = 3 108 m/s
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Porcentagem
Como citar este documento: GONÇALVES, Claudio Daniel Porto; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Aritmética. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/aritmetica.html. Acesso em: [data de acesso].
Podemos expressar quantidades em forma de porcentagem com o uso do símbolo (%). Considere a razão ( ) novamente.
ou 2 : 5 ou 0,4 ou 40%
Dizemos que a notação 40% é percentual, e a notação 0,4 é decimal, para realizarmos os cálculos que envolvam percentual usaremos a notação decimal.
O valor de 40% significa que o numerador da fração, o número 2, representa 40% do denominador, o número 5. Isso quer dizer que se quisermos retirar 40% de um total de 5 unidades, obteremos 2 unidades, e restarão 3 unidades, ou seja 60%.
E como podemos obter uma fórmula para obter a porcentagem de determinada quantidade de alguma grandeza? Consideremos as seguintes ideias, temos uma quantidade total denotada por (Qt), e queremos determinar a quantidade (Q) que teremos com P%, onde P% representa a porcentagem. Então obteremos a seguinte fórmula:
Q = P% Qt (I)
Onde,
Q: quantidade correspondente à porcentagem %P
Qt: quantidade total
P%: porcentagem referente a quantidade Q
Se quisermos determinar quanto é 10% de 80, é só substituirmos os valores na fórmula (I), onde Qt é 80, e P% é 10%.
Q = 10% 80
No entanto não podemos realizar cálculos com 10%, mas sabemos que 10% equivale a 0,1. Então obtemos:
Q = 0,1 80
Q = 8
Agora faremos manipulações na equação (1), para obtermos expressões que calculam P% e Qt. Primeiro iremos determinar P%, para isso iremos dividir os dois lados da equação (1) por Qt, a fim de isolar P%.
Q = P%
Qt
.
P% =
Com essa fórmula podemos calcular, por exemplo, qual é a porcentagem que 10 representa em uma quantidade total de 80.
P% = = 0,125 = 12,5%
Agora se quisermos calcular a quantidade total Qt, dividimos os dois lados da equação (1) por P%.
Q = P%
Qt
Qt =
Se por exemplo sabemos que 12 unidades de uma determinada quantidade, representam 15% da quantidade total, podemos usar a fórmula (3) para determinarmos qual é a quantidade total:
Qt =
Qt = 80 unidades
EXERCÍCIOS
13 - Calcule.
-
15% de 800
-
2% de 1250
-
85% de 16
-
68% de 220
-
125% de 560
-
370% de 58
-
0,1% de 500
-
0,002% de 100.000
-
1200% de 5
14 - Considere uma sala de aula com 80 alunos, 50 meninas e 30 meninos.
a. Qual a porcentagem do número de meninas em relação ao número de alunos?
b. Qual a porcentagem do número de meninos em relação ao número de alunos?
c. Qual a porcentagem do número de meninas em relação ao número de meninos?
d. Qual a porcentagem do número de meninos em relação ao número de meninas?
15 – Calcule.
(a) Quantos por centos 50 é de 250?
(b) Quantos por centos 225 é de 1500?
(c) Quantos por centos 60 é de 20?
(d) Quantos por centos 0,4 é de 160?
(e) Quantos por centos 1000 é de 50?
16 – Uma cidade tem sua população aumentada de 120.500 pessoas para 150.000, qual foi o aumento percentual da população nesta cidade?
17 - Em um estante de livros, 20 são de física, 15 de química e 40 são de matemática.
Figura 53 – Estante com livros.
Fonte: Pixabay (2016) (https://pixabay.com/)
Responda, qual a porcentagem.
-
Dos livros de física em relação ao número total de livros.
-
Dos livros de química em relação ao número total de livros.
-
Dos livros de matemática em relação ao número total de livros.
APLICAÇÕES
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021