Contextualização

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

Os triângulos são as primeiras figuras planas com que temos contato, já que são necessários no mínimo três vértices e três lados para formar um polígono. Sendo assim, os triângulos são os polígonos mais simples, porém muito importantes, devido a sua incidência nos vestibulares e a sua presença em monumentos históricos e em construções arquitetônicas, como podemos ver a seguir:

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Triângulo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

Triângulo é toda figura plana que possui três vértices, três lados e três ângulos.

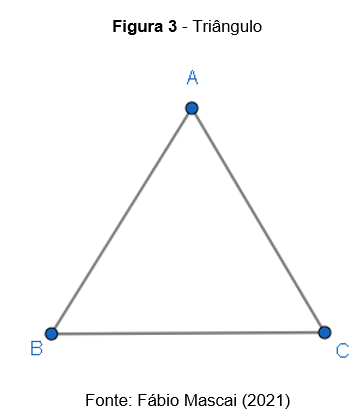
Os elementos do triângulo são:

1. Vértices: os pontos A, B e C

2. Lados: os segmentos  ,  e 

3. Ângulos Internos:  ,  e  B
   
   
   Base de um Triângulo

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Ângulo Externo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

Se, por exemplo, prolongarmos um dos lados de um triângulo, o ângulo formado entre esse prolongamento e o lado seguinte é chamado ângulo externo do triângulo.


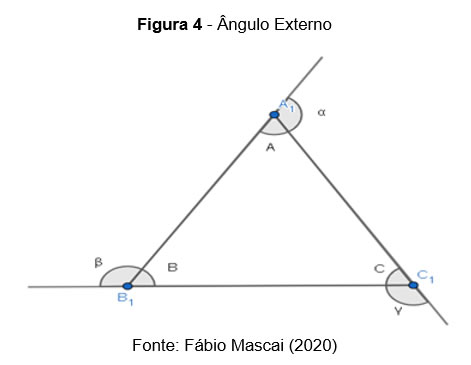
Na figura, os ângulos de medidas  ,  e  são ângulos externos do triângulo  .

Cada um dos ângulos externos é suplementar ao seu respectivo ângulo interno.

 

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Soma dos Ângulos Internos

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

A soma dos ângulos internos de qualquer triângulo é sempre igual a   .

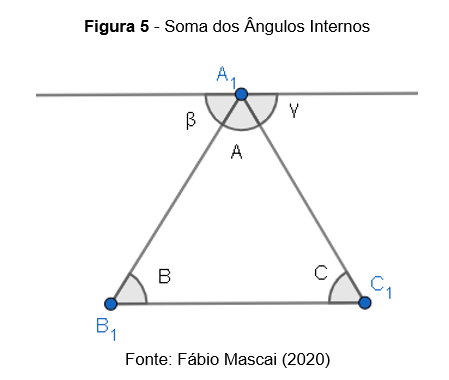
Trabalhando com paralelismo e suas consequências, podemos dizer que os ângulos de medidas  e  são, respectivamente, congruentes aos ângulos  e  (ângulos alternos internos)

   

 

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Soma dos Ângulos Externos

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

A soma dos ângulos externos de qualquer triângulo é sempre igual a 

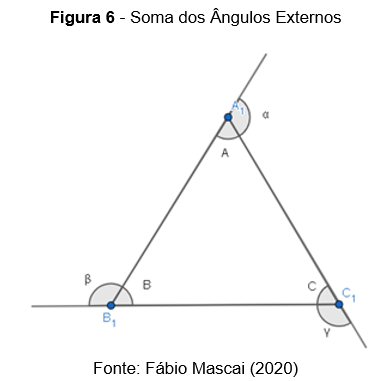
Vimos que os ângulos externos e os ângulos internos são suplementares, portanto:

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Teorema do Ângulo Externo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

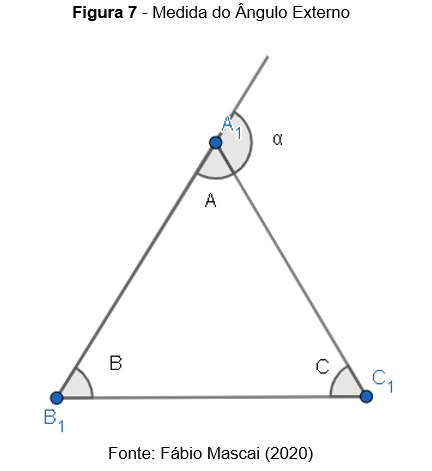
Em qualquer triângulo, a medida de cada ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes.

 

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Classificação dos Triângulos

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

Quanto aos lados, podemos ter:

Triangulo Equilátero: possuí todos os lados congruentes:

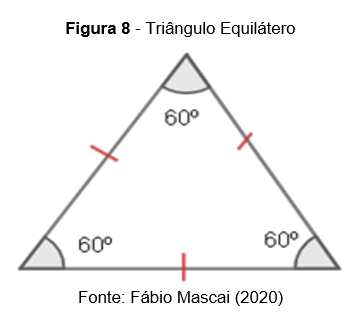
Todo triângulo equilátero também é equiângulo, ou seja, possui todos os ângulos congruentes, sendo que cada um deles mede 

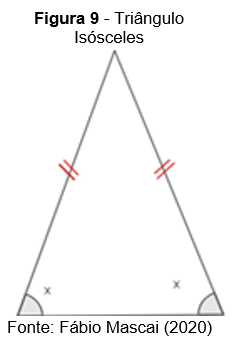
Chamando de α a medida de cada ângulo do triângulo equilátero,temos:






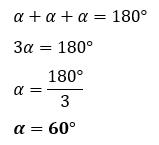
Triângulo Isósceles: possuí dois lados congruentes, sendo que o lado não congruente é comumente chamado de base

Todo triângulo isósceles é também isoângulo, ou seja, possui os ângulos da base congruentes

 

Triângulo Escaleno: possui todos os lados com medidas diferentes

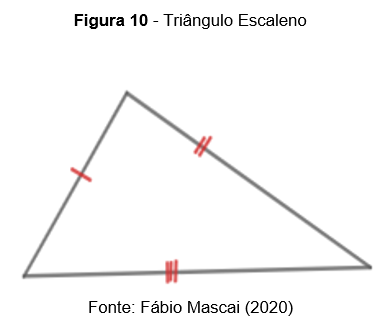
Não há nenhuma congruência nesse tipo de triângulo

• Quanto aos ângulos, podemos ter:
  
  

 Triângulo acutângulo: possui todos os ângulos agudos, ou seja, menores que  

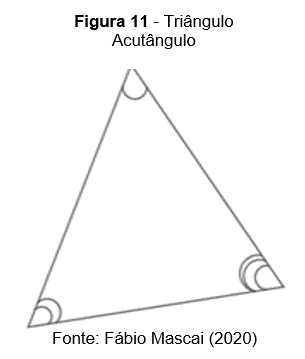
Triângulo Obtusângulo: possui um ângulo obtuso, ou seja, maior que  ( )

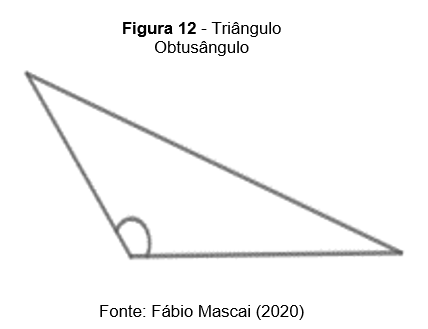
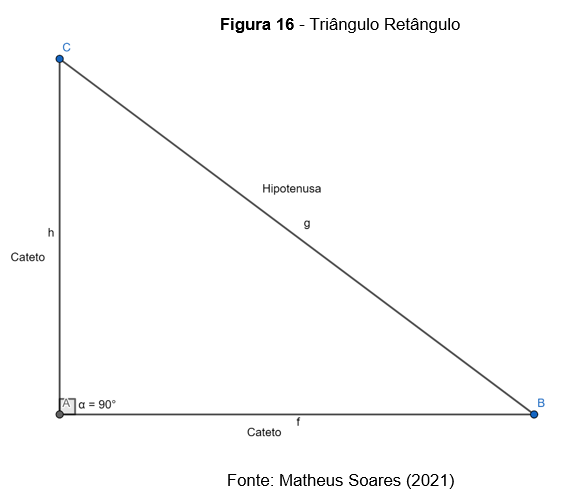
Triângulo Retângulo: possui um ângulo reto, ou seja, com a medida igual a 

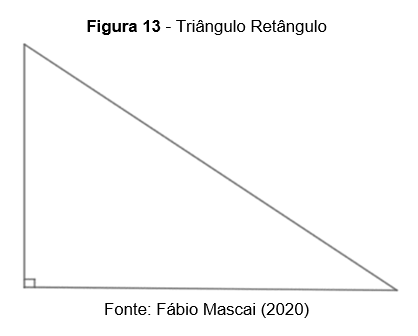
O maior lado de um triângulo retângulo é chamado hipotenusa e ele é oposto ao ângulo de   ; os outros dois lados são chamados catetos

Trigonometria

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Cevianas do Triângulo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

 

As cevianas de um triângulo são segmentos de reta que partem de um dos vértices desse triângulo e encontram o lado oposto a esse vértice.

São elas: a altura, a mediana e a bissetriz interna.

Elas serão particularmente importantes para o nosso estudo quando chegarmos em pontos notáveis de um triângulo.

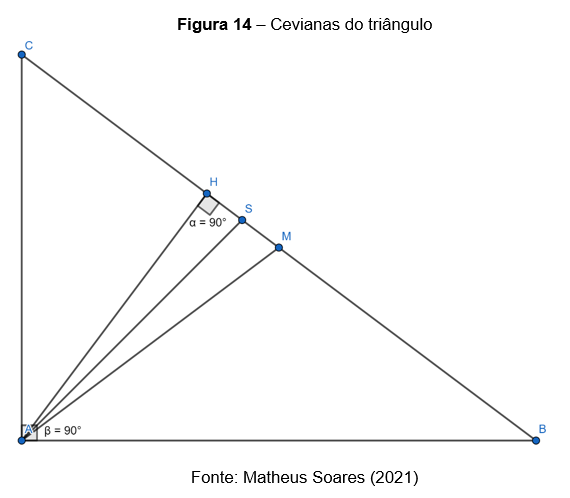
Na figura, temos:
 = altura

 = mediana

 = bissetriz interna

• Altura: é o segmento de reta que parte de um dos vértices do triângulo e encontra perpendicularmente o lado oposto, ou seja, a altura forma ângulos de 

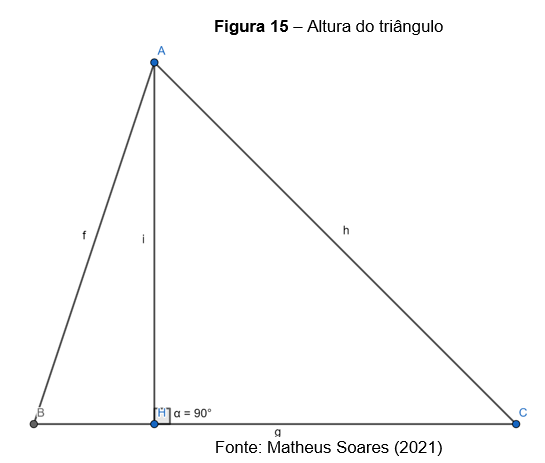
Na figura, o segmento de reta  é uma altura do triângulo ABC, pois ela parte do vértice A, encontra o lado  no ponto H e é perpendicular ao lado  .

Um triângulo possui três alturas, uma para cada vértice

Num triângulo retângulo, cada cateto é a altura relativa ao outro cateto

Num triângulo obtusângulo, a altura pode ser um segmento de reta externo ao triângulo

• Mediana: é o segmento de reta que une um vértice ao ponto médio do lado oposto a esse vértice

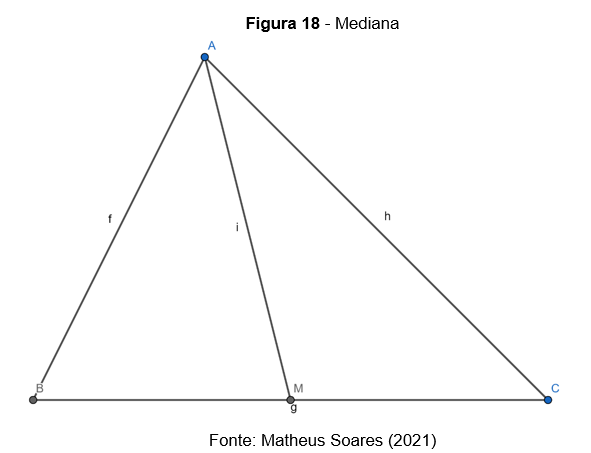
Na figura, o segmento de reta  é uma mediana do triângulo ABC, pois une o vértice A ao ponto médio (M) do lado 

Como M é o ponto médio do lado  , temos que  é congruente a  e, portanto: 

Um triângulo possui três medianas, uma para cada vértice

• Bissetriz interna: é o segmento de reta que une um vértice a um ponto do lado oposto e divide o ângulo interno desse vértice ao meio

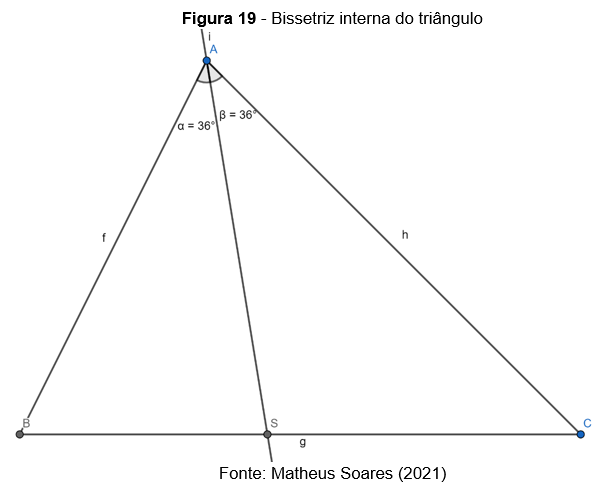
Na figura, o segmento de reta  é uma bissetriz interna do triângulo ABC, pois ela parte do vértice A, encontra o lado  no ponto S e divide o ângulo  ao meio.

Um triângulo possui três bissetrizes internas, uma para cada vértice

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Exercícios Resolvidos

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Triângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/triangulos.html. Acesso em: [data de acesso].

 

R1. O triângulo da figura é:

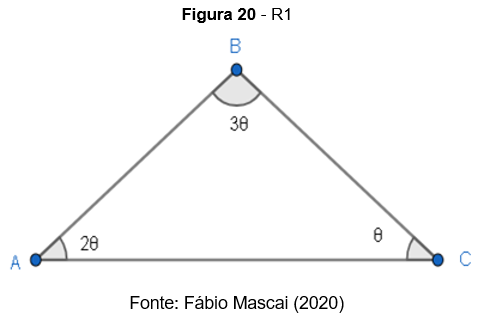
1. Acutângulo e escaleno
2. Retângulo e escaleno
3. Obtusângulo e escaleno
4. Acutângulo e equilátero
5. Retângulo e isósceles
   

R2.  Calcule a medida do ângulo externo na figura

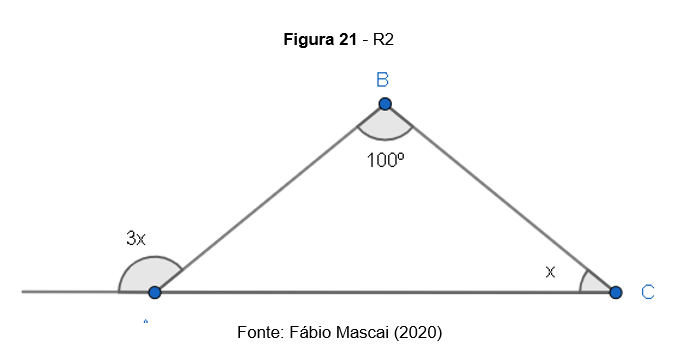
R3. Encontre o valor de x

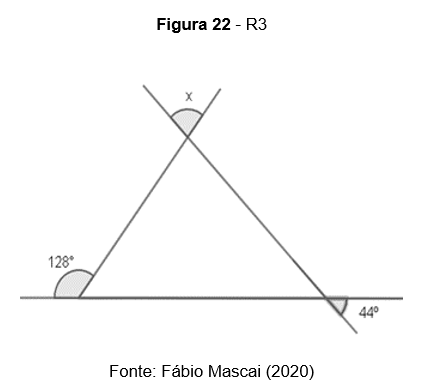
Chamando de α e β os ângulos internos do triângulo não adjacentes ao ângulo externo de 128°,temos:

R4. Sobre as propriedades dos triângulos, assinale a alternativa correta:

1. A soma dos ângulos internos de um triângulo retângulo é diferente de
2. A soma dos ângulos externos de um polígono depende da quantidade de lados que ele possui
3. O maior lado de um triângulo sempre é oposto ao seu maior ângulo. O menor lado de um triângulo sempre é oposto ao seu menor ângulo
4. Os ângulos da base de um triângulo isósceles medem
5. Em um triângulo isósceles, todos os lados são congruentes

Exercícios Propostos

P1. Calcule o valor de x

1. 

2. 

3. 

4. 

5. 

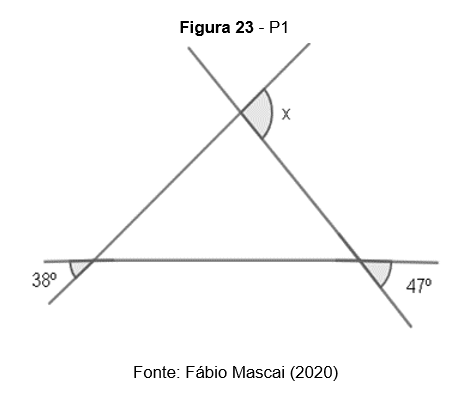
P2. Calcule o valor de x

1. 

2. 

3. 

4. 

5. 

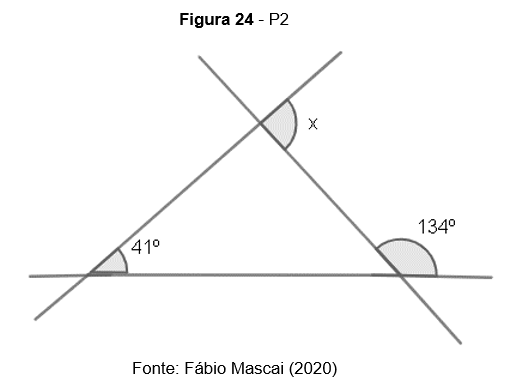
P3. Calcule o valor de x

1. 

2. 

3. 

4. 

5. 

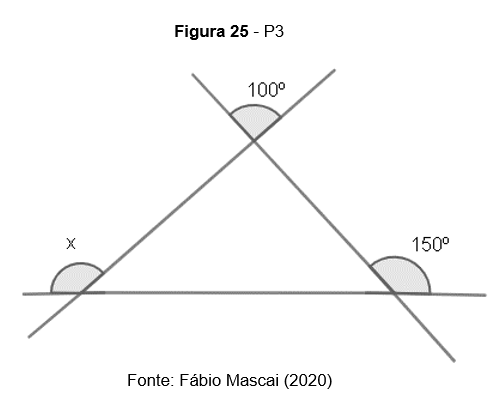
P4. (Modelo ENEM) Se a medida de um ângulo interno de um triângulo é igual à soma das medidas dos outros dois ângulos internos, então, necessariamente, esse triângulo:

1. É retângulo

2. É equilátero

3. Tem lados de medidas 3,4 e 5

4. É isósceles sem ser equilátero

5. Tem um ângulo interno de 

P5. Na figura, o ângulo  mede:

1. 

2. 

3. 

4. 

5. 

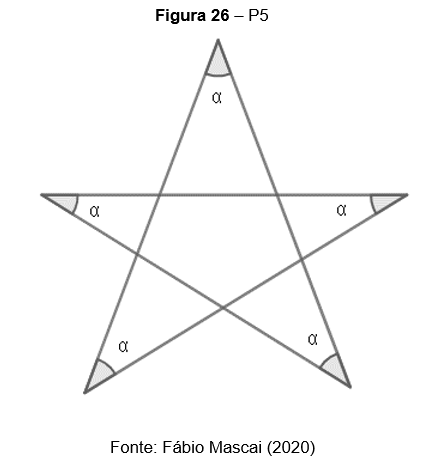
P6. Na figura, AB=BD=CD. Então:

1. 

2. 

3. 

4. 

5. 

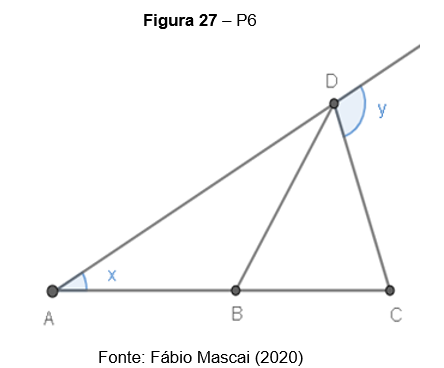
P7. Na figura abaixo, tem-se que AD=AE, CD=CF e BA=BC. Se o ângulo   mede   , então o ângulo   mede:

1. 

2. 

3. 

4. 

5. 

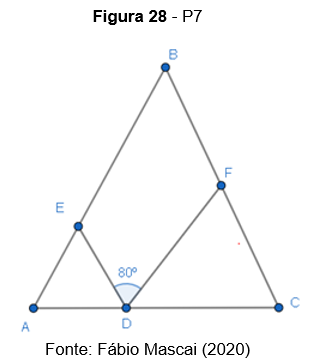
P8. Na figura seguinte, tem-se AB=BC=CD=DE=EF. Determine a medida do ângulo   , dado que a medida do ângulo   é igual a 

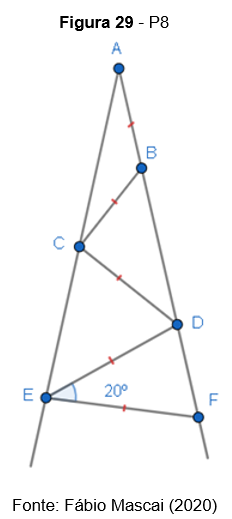
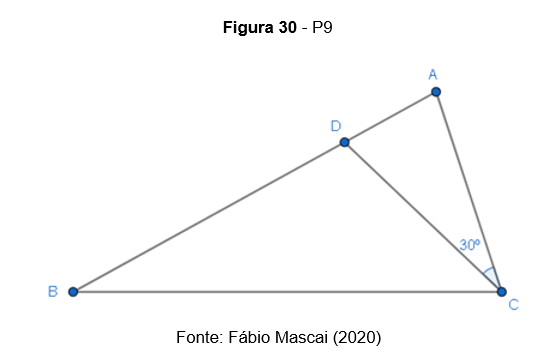
P9. (Mackenzie – SP) No triângulo abaixo, temos AB=BC e AC=CD. Se x e y são as medidas em graus dos ângulos   e   , respectivamente, então x+y é igual a:

1. 

2. 

3. 

4. 

5. 

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021