
POTENCIAL ELÉTRICO
IFSP - Cursinho Popular
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Tópicos: Conteúdo programático; Trabalho Força Elétrica; Energia Potencial Elétrica; Potencial Elétrico; Tensão Elétrica; Linha de Força; Campo Elétrico Uniforme; Equilíbrio Eletrostático; Exercícios e Bibliografia.
Conteúdo Programático
1. Trabalho
2. Trabalho realizado pela Força Elétrica
3. Energia Potencial Elétrica de um sistema
4. Potencial elétrico gerado por cargas puntiformes
5. Linhas de força geradas por cargas puntiformes
6. Diferença de potencial elétrico entre dois pontos
7. Campo elétrico entre placas paralelas eletrizadas
8. Diferença de potencial elétrico entre placas paralelas eletrizadas
9. Potencial de condutor em equilíbrio eletrostático
10. Superfícies equipotenciais
Objetivos deste texto
A partir da leitura deste texto, esperamos que você possa:
I) Compreender o que a Física caracteriza como trabalho;
II) Compreender como se calcula o trabalho realizado pela força elétrica;
III) Interpretar adequadamente o significado da energia potencial elétrica associada a um sistema;
IV) Notar a relevância do conceito de potencial elétrico por sua independência em relação à existência ou não de um corpo de prova;
V) Compreender como se calcula o potencial elétrico gerado por cargas elétricas em diferentes situações;
VI) Identificar a diferença de potencial elétrico (tensão elétrica) como maneira de fornecer energia às cargas elétricas;
VII) Relacionar a tensão elétrica com o funcionamento de aparelhos eletroeletrônicos com os quais lidamos no dia a dia.
VIII) Compreender os conceitos de linhas de força e de superfícies equipotenciais.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
TRABALHO DA FORÇA ELÉTRICA
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Um dos princípios básicos da Física é a noção de energia, que pode ser transformada ou transferida, mas nunca criada ou destruída. No nosso cotidiano, deparamo-nos com diversos tipos de energia: energia mecânica, energia elétrica, energia térmica, entre outras. A utilização da energia é de extrema importância para a humanidade, por meio de sua transferência ou transformação. Atualmente, a energia proveniente de combustões, de quedas de água, de reações químicas ou até mesmo do núcleo atômico é utilizada, entre outras coisas, para fazer funcionar fábricas, meios de transportes mecanizados e aparelhos elétricos. Embora não seja nada simples caracterizar o que é , em certas circunstâncias, podemos relacioná-la diretamente com a capacidade de produzir movimento, de gerar trabalho. Mas o que é o trabalho? Diferentemente do significado atribuído habitualmente a essa palavra, o trabalho, na Física, é uma grandeza que mede a quantidade de energia transferida ou transformada pela aplicação de uma força (gravitacional, elétrica, magnética etc.) ao longo de um deslocamento. Assim como ocorre com a energia, sua unidade de medida no Sistema Internacional (SI) é o . Logo, existem duas condições para que ocorra trabalho: 1) a existência de uma força ou de uma componente de força (decomposição do vetor força) na direção do deslocamento; 2) que essa força ou componente de força cause o deslocamento do corpo.
Caso a força que está causando o deslocamento de um corpo seja constante, podemos calcular o trabalho utilizando a seguinte fórmula:
![]()
Em que:
é o trabalho realizado (em Joule - J);
F é a força aplicada no corpo (em Newton - N);
d é deslocamento do corpo (em metro, m);
θ é o ângulo formado entre as direções da força aplicada e do deslocamento.
Quando o deslocamento e a força (ou seu componente) têm o mesmo sentido, dizemos que o trabalho é motor. Nesse caso, a força está atuando de forma a transferir energia para o corpo. No caso de o deslocamento e a força (ou, novamente, seu componente) terem sentidos opostos, o trabalho é dito resistente. Nesse caso, a força está atuando de forma a retirar energia do corpo.
Consideremos, a partir de agora, o campo elétrico gerado por um corpo fixo Q eletrizado com carga elétrica positiva. Se abandonarmos nessa região uma carga de prova q, ela sofrerá uma força de interação de natureza elétricaFigura 1 - Deslocamento de uma carga q inserida em um campo elétrico gerado por uma carga Q
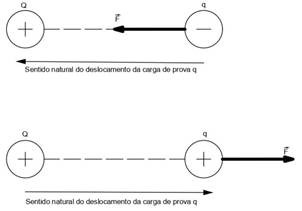
Fonte: Luiz Setti/Arquivo pessoal
Note que no exemplo dado, a energia capaz de realizar trabalho (causar o deslocamento do corpo por meio da aplicação de uma força) se encontra de alguma forma armazenada no sistema, isto é, se encontra na forma de energia potencial.
É importante entender que o trabalho da força elétrica não depende da trajetória da carga de prova, mas sim dos pontos inicial e final de seu deslocamento. Isso decorre do fato de a força elétrica ser uma força conservativa. Em outras palavras: sua atuação não implica na transformação de energia mecânica do corpo em outros tipos de energia (energia térmica, por exemplo). A força de atrito é um exemplo de força não conservativa ou força dissipativa.
Na Figura 2, temos um exemplo em que a carga de prova q percorreu trajetórias diferentes para se deslocar de um ponto a outro por meio da ação de uma força elétrica. O trabalho realizado pela força elétrica é igual em todos esses deslocamentos.
Figura 2 - Trabalho da força elétrica em trajetórias diversas
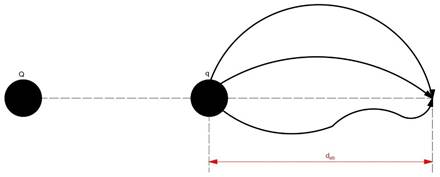
Fonte: Luiz Setti/Arquivo pessoal
Vamos novamente considerar o campo elétrico criado por um corpo fixo Q carregado eletricamente e uma carga de prova q se movendo de um ponto A para um ponto B devido à ação da força elétrica (Figura 3).
Figura 3 - Trabalho da força elétrica
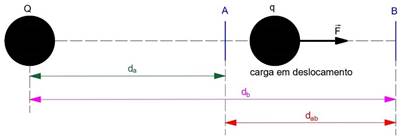
Fonte: Luiz Setti/Arquivo pessoal
Em casos como esse não será possível utilizar a fórmula geral para o cálculo do trabalho (![]() ), porque a força elétrica não é constante entre os pontos A e B - ela varia conforme a distância entre as cargas (Fel = k.Q.q/d2). Contudo, ao lembrarmos que o trabalho de forças conservativas depende apenas dos pontos inicial e final da trajetória, poderemos calcular o trabalho da força elétrica usando a seguinte equação:
), porque a força elétrica não é constante entre os pontos A e B - ela varia conforme a distância entre as cargas (Fel = k.Q.q/d2). Contudo, ao lembrarmos que o trabalho de forças conservativas depende apenas dos pontos inicial e final da trajetória, poderemos calcular o trabalho da força elétrica usando a seguinte equação:
![]()
Onde:
Wel é o trabalho da força elétrica (medido em J);
k é a constante eletrostática, cujo valor no vácuo é de 9.109 Nm2/C;
Q é o valor da carga elétrica de Q (medida em C);
q é o valor da carga elétrica de prova (medida em C);
dA é a distância da carga Q até o ponto de início do movimento da carga q (medida em m);
dB é a distância da carga Q até o ponto final do movimento da carga q (medida em m).
EXERCÍCIO RESOLVIDO 1
Considere o campo criado pela carga puntiforme Q = 2.10-6 C no vácuo, conforme a Figura 4. Determine o trabalho realizado pela força elétrica para deslocar uma carga de prova q = 10.10-8 C de A para B.
Figura 4 - Exercício 1
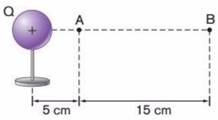
Fonte: Bonjorno et al. (2016)
Dados:
![]()
![]()
![]()
![]()
![]()
Sabemos que o trabalho da força elétrica pode ser calculado através da fórmula:
![]()
Portanto, substituindo os valores, tem-se:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 2
Considere o campo criado pela carga puntiforme Q = 4.10-6 C no vácuo, conforme a Figura 5. Sabendo que o trabalho realizado pela força elétrica para deslocar uma carga de prova q do ponto A para o ponto B é de 2,88 J, determine q.
Figura 5 - Exercício 2
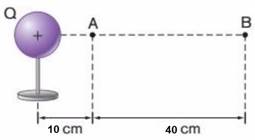
Fonte: Adaptado de Bonjorno et al. (2016)
Dados:
![]()
![]()
![]()
![]()
![]()
Utilizaremos a fórmula:
![]()
Substituindo:
![]()
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 3
Os pontos A, B, C e D estão no campo elétrico de uma carga puntiforme Q, fixa, conforme a Figura 6. Transportando-se uma carga de prova q de A até B pelo caminho 1, as forças elétricas realizam um trabalho. Determine o trabalho realizado pelas forças elétricas para transportar a mesma carga q de A até B nas condições anteriores pelos caminhos 2 e 3.
Figura 6 - Exercício 3
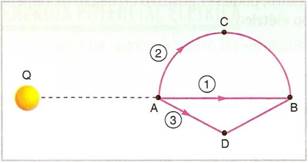
Fonte: Bonjorno et al. (2001)
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
ENERGIA POTENCIAL ELÉTRICA
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Na Figura 7, temos uma carga fixa Q e uma carga de prova q separadas, inicialmente por uma distância dA. Vamos supor que o ponto B está infinitamente afastado da carga fixa geradora do campo elétrico, isto é, dB tende a um valor infinito.
Figura 7 - Energia potencial elétrica
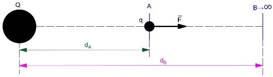
Fonte: Luiz Setti/Arquivo pessoal
![]()
![]()
![]()
![]()
![]()
Além disso, vemos que o trabalho realizado por uma força elétrica para movimentar uma carga de prova de um ponto A a um ponto B é igual à diferença entre as energias potenciais do sistema associadas a tais pontos. Ou seja:
![]()
![]()
![]()
![]()
Lembrando que, na Física, o símbolo Δ (delta) indica variação, final menos inicial. Nesse caso: energia potencial em B menos energia potencial em A.
EXERCÍCIO RESOLVIDO 4
Em um campo elétrico, uma carga de prova é levada de um ponto A, distante 5 mm da carga fixa Q, geradora do campo elétrico, até um ponto B muito afastado. Considere que o evento ocorreu no vácuo e que q=15 μC e Q=300 μC. Determine a energia potencial do sistema quando a carga de prova está em A.
Dados:
![]()
![]()
![]()
![]()
![]()
Como o ponto B tende a uma distância infinita da carga Q, utilizaremos a fórmula:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 5
Uma carga de prova carregada eletricamente deslocou-se de um ponto A para um ponto B dentro de um campo elétrico. A energia potencial associada ao sistema em A foi calculada em 150 J. Em B, o valor calculado para a energia potencial do sistema foi de 1 J. Qual foi o trabalho exercido pela força elétrica para deslocar essa partícula nessas condições?
Dados:
![]()
![]()
Sabemos que a força elétrica é uma força conservativa, por isso o trabalho é o resultado da diferença entre as energias potenciais nos dois pontos:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 6
Determine a energia potencial associada a um sistema quando uma carga de 5 μC é colocada a 7,2 cm de uma carga de 0,2 μC, fixa, localizada no vácuo.
Dados:
![]()
![]()
![]()
![]()
A energia potencial é calculada pela fórmula:
![]()
![]()
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
POTENCIAL ELÉTRICO
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Como vimos, em um campo elétrico criado por um corpo fixo Q carregado eletricamente, a energia potencial que pode ser associada ao sistema quando uma partícula eletrizada se localiza num ponto A é diretamente proporcional ao valor de sua carga elétrica (q). Para exemplificar, na Figura 8, temos uma carga fixa Q e, equidistantes dela, três pontos distintos P1, P2 e P3, onde se encontram, respectivamente, as cargas de prova q1, q2 e q3.
Figura 8 - Potencial elétrico
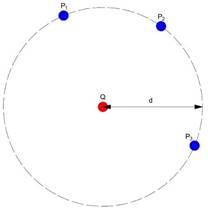
Fonte: Luiz Setti/Arquivo pessoal
Para calcularmos a energia potencial em cada dos pontos supracitados, teremos:
![]()
![]()
![]()
![]()
Ou, também:
![]()
O gráfico do potencial elétrico em função da distância está representado nas Figuras 9 e 10. A curva formada é chamada de hipérbole equilátera. Se a carga for positiva, a curva será no primeiro quadrante de um plano cartesiano (Figura 9); no caso de a carga ser negativa, a curva aparecerá no quarto quadrante de um plano cartesiano (Figura 10).
Figura 9 - Gráfico do potencial elétrico de uma carga puntiforme positiva em função da distância
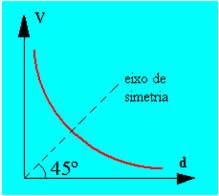
Fonte: SILVA (20--?) (https://mundoeducacao.uol.com.br/fisica/grafico-potencial-eletrico.htm)
Figura 10 - Gráfico do potencial elétrico de uma carga puntiforme negativa em função da distância
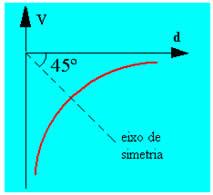
Fonte: SILVA (20--?) (https://mundoeducacao.uol.com.br/fisica/grafico-potencial-eletrico.htm)
No caso de existirem vários campos elétricos agindo numa região, o potencial elétrico em um ponto qualquer é a soma algébrica de todos os potenciais elétricos associados a ele:
![]()
Por exemplo: o potencial elétrico no ponto P da Figura 11 é a soma algébrica dos potenciais associados aos campos elétricos gerados pelos três corpos eletricamente carregados envolvidos na situação.
Figura 11 - Potencial gerado por várias cargas elétricas
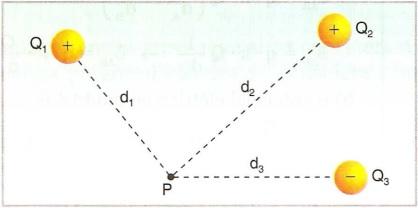
Fonte: Bonjorno et al. (2001)
EXERCÍCIO RESOLVIDO 7
Determinar o potencial elétrico em um ponto P situado no vácuo a 40 cm de uma carga elétrica puntiforme de 8 μC.
Dados:
![]()
![]()
![]()
Para achar o potencial elétrico, utilizaremos a fórmula:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 8
Determinar o potencial no ponto P no vácuo, devido às cargas puntiformes Q1, Q2 e Q3, cujos valores são 4 μC, 8 μC e -2 μC, respectivamente (Figura 13). Considere θ=90°.
Figura 12 - Exercício 8
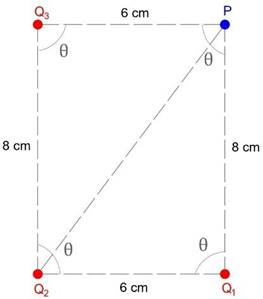
Fonte: Luiz Setti/Arquivo pessoal
Dados:
![]()
![]()
![]()
![]()
![]()
![]()
Como a figura formada é um triângulo retângulo, por causa de θ ser igual a 90 graus, calcularemos a distância entre Q2 e P (hipotenusa desse triângulo) utilizando o teorema de Pitágoras:
![]()
![]()
![]()
![]()
Agora, deve-se calcular o potencial elétrico produzido por cada carga:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Para calcular o potencial total, deveremos somar cada um dos valores encontrados:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 9
No campo eletrostático de uma carga puntiforme Q=4 μC, fixa no vácuo, são dados dois pontos A e B, cujas distâncias em relação à carga são, respectivamente, 20 cm e 60 cm, como mostra a Figura 13. Dado k=ko=9.109 Nm2/C2, calcule os potenciais elétricos nos pontos A e B.
Figura 13 - Exercício 9
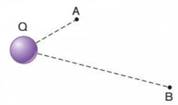
Fonte: Bonjorno et al. (2016)
Dados:
![]()
![]()
![]()
![]()
Calculando o potencial elétrico em A:
![]()
![]()
![]()
![]()
E, agora, calcularemos o potencial elétrico em B:
![]()
![]()
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
DIFERENÇA DE POTENCIAL ELÉTRICO (D.D.P.)
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
A diferença de potencial elétrico, também chamada de tensão elétrica ou voltagem, é uma grandeza física muito relevante na eletricidade. A partir dela, explica-se o movimento das cargas elétricas na corrente elétrica. Sua unidade de medida no SI é o Volt (V).
Na Figura 14, podemos observar uma carga fixa Q, criadora de um campo elétrico, e uma carga de prova q que se desloca do ponto A para o ponto B.
Figura 14 - Diferença de Potencial Elétrico

Fonte: Luiz Setti/Arquivo pessoal
O trabalho realizado pela força elétrica para mover essa carga de prova é:
![]()
Como:
![]()
Então:
![]()
![]()
![]()
Portanto:
![]()
![]() = -
= -![]()
O termo ![]() é a diferença de potencial elétrico (ddp) entre os pontos A e B. Podemos denominar, também, como tensão elétrica entre A e B. A ddp entre dois pontos costuma ser representada pela letra U. Logo:
é a diferença de potencial elétrico (ddp) entre os pontos A e B. Podemos denominar, também, como tensão elétrica entre A e B. A ddp entre dois pontos costuma ser representada pela letra U. Logo:
![]() =
= ![]()
![]() ou
ou ![]()
Note que ao escrevermos A ![]() B estamos indicando que os pontos inicial e final são, respectivamente, os pontos A e B. Já ao escrevermos B
B estamos indicando que os pontos inicial e final são, respectivamente, os pontos A e B. Já ao escrevermos B ![]() A estamos indicando que os pontos inicial e final são, respectivamente, os pontos B e A. Logo: UB
A estamos indicando que os pontos inicial e final são, respectivamente, os pontos B e A. Logo: UB![]() A = VA – VB e, por outro lado, UA
A = VA – VB e, por outro lado, UA![]() B = VB – VA.
B = VB – VA.
EXERCÍCIO RESOLVIDO 10
O trabalho realizado pela força elétrica para deslocar uma partícula carregada eletricamente é de 103,4 μJ. Sabendo que essa partícula possui uma carga de 470 nC, determine a tensão elétrica do circuito.
Dados:
![]()
![]()
Para calcular a tensão elétrica (ddp), utilizaremos a fórmula:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 11
A energia potencial num determinado ponto de um campo elétrico é 3,858 mJ. Já em um segundo ponto a uma certa distância, a energia potencial passa a valer 858 μJ. Foi inserida no primeiro ponto uma partícula com carga elétrica de 3 mC. Sabendo que essa partícula se deslocou até o segundo ponto citado, calcule a diferença de potencial elétrico entre esses dois pontos e o trabalho realizado pela força elétrica nesse deslocamento.
Dados:
![]()
![]()
![]()
Para obtermos o valor do trabalho elétrico:
![]()
![]()
![]()
O valor da tensão elétrica vem da seguinte relação:
![]()
E como:
![]()
![]()
![]()
![]()
![]()
![]()
Portanto:
![]()
![]()
![]()
Note que o sinal negativo indica que o potencial elétrico de B é menor que o potencial elétrico de A. Ou seja: a tensão entre os pontos A (inicial) e B (final) é negativa. Outra forma de pensar é: quando a partícula vai do ponto A ao ponto B o sistema perde energia potencial elétrica e essa energia aparece na forma de trabalho (usado para movimentar a partícula entre os referidos pontos).
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
POTENCIAL ELÉTRICO NUMA LINHA DE FORÇA
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Uma carga puntiforme positiva fixa gera um campo elétrico com linhas de força de afastamento a partir de Q (Figura 15).
Figura 15 - Linha de força gerada por uma carga fixa Q positiva

Fonte: Luiz Setti/Arquivo pessoal
Para calcularmos os potenciais elétricos nos pontos A, B, C e D, usamos a seguinte fórmula:
![]()
Como:
![]()
Teremos como consequência da fórmula:
![]()
Figura 16 -Variação do potencial elétrico ao longo de uma linha de força
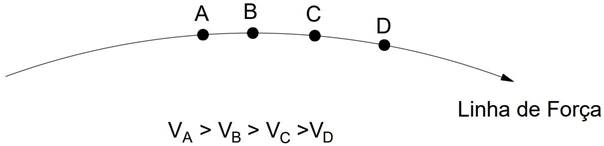
Fonte: Luiz Setti/Arquivo pessoal
Agora, se soltarmos uma carga de prova q positiva no ponto C, por exemplo, ela irá se movimentar espontaneamente para o ponto D, que tem menor potencial. Caso a carga seja negativa, dentro do mesmo exemplo acima, o deslocamento será para o ponto B, de maior potencial.
Portanto, tomando um ponto como referencial, ao analisarmos a linha de força de um campo elétrico, obteremos diferentes potenciais, com valores cada vez menores conforme nos distanciamos desse ponto de referência (Figura 16). Caso a carga que origina o campo elétrico seja negativa, as linhas de força do campo elétrico são de aproximação. Ainda assim, caso façamos análise similar à feita nos parágrafos anteriores, chegaremos à mesma conclusão: partículas com cargas elétricas positivas se movimentam espontaneamente para pontos de menor potencial elétrico e partículas com cargas elétricas negativas se movimentam espontaneamente para pontos de maior potencial elétrico.
EXERCÍCIO RESOLVIDO 12
Uma partícula de carga 4 C é abandonada a partir do repouso no ponto A do campo elétrico criado pela carga positiva Q, conforme a Figura 17. Sabendo que os potenciais elétricos em A e B são, respectivamente, 1000 V e 700 V, determine a energia potencial elétrica da partícula nos pontos A e B, e o trabalho para que ela se desloque de A para B.
Figura 17 - Exercício 12

Fonte: Luiz Setti/Arquivo pessoal
Dados:
![]()
![]()
![]()
A energia potencial será calculada por:
![]()
![]()
![]()
![]()
![]()
![]()
Há mais de uma forma para obtermos o trabalho dessa força elétrica. Usaremos a fórmula:
![]()
Portanto:
![]()
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
DDP NUM CAMPO ELÉTRICO UNIFORME
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Na Figura 18, temos duas placas eletrizadas com cargas de mesmo módulo, mas inversamente polarizadas, e paralelas uma à outra, separadas por uma distância d. Considere que esse campo elétrico é uniforme.
Figura 18 - Campo elétrico criado por duas placas eletrizadas paralelas
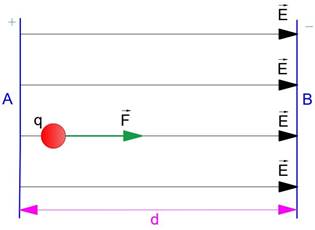
Fonte: Luiz Setti/Arquivo pessoal
A carga de prova positiva q inserida entre essas placas irá se deslocar de A para B. O trabalho realizado pela força elétrica é:
![]() =
= ![]() =
= ![]()
Levando em conta que a força
![]() .cosθ = F.dA
.cosθ = F.dA![]() B (já que θ = 0°
B (já que θ = 0° ![]() cos 0° = 1)
cos 0° = 1)
E a relação entre campo e força elétrica é expressa pela seguinte equação:
![]()
Logo:
![]()
Agora, iremos igualar as EQUAÇÕES I e II:
![]()
![]()
Sabemos que:
![]()
Portanto:
![]()
Ou
![]()
Caso não estejamos preocupados com qual dos dois pontos em questão tem maior/menor potencial elétrico e tampouco com o sentido do campo elétrico uniforme, podemos simplesmente escrever que: U = E.d.
Por análise dimensional dessa equação, percebemos que o campo elétrico, além de ser medido em N/C (Newton por Coulomb) pode ser medido também em Volt por metro (V/m).
EXERCÍCIOS RESOLVIDO 13
Determinar a ddp entre os pontos A e B de um campo elétrico uniforme de intensidade igual a 105 N/C, sabendo-se que a distância entre esses pontos é de 0,2 cm.
Dados:
![]()
![]()
Pelo fato de ser um campo elétrico uniforme, utilizaremos a equação:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 14
Uma carga elétrica de 6.10-12 C é abandonada em um ponto A de um campo elétrico uniforme atingindo um ponto B, conforme a Figura 19. Determine a intensidade do campo elétrico, sabendo que VA = 500 V; VB = 100 V; e que a distância entre os pontos A e B é d = 0,002 m.
Figura 19 - Exercício 14
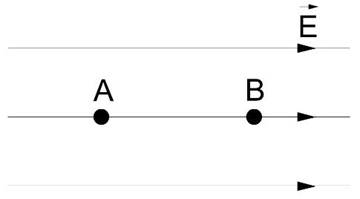
Fonte: Luiz Setti/Arquivo pessoal
Dados:
![]()
![]()
![]()
Primeiro, calcularemos a tensão elétrica (ddp):
![]()
![]()
![]()
Mais uma vez, o campo elétrico é uniforme, partiremos com a equação:
![]()
ou
![]()
- ![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 15
Uma partícula de carga q = 2 μC está situada em um campo eletrostático uniforme de intensidade E = 2.104 V/m. Qual o trabalho da força elétrica necessário para deslocar essa partícula em 0,5 m no sentido do campo?
Dados:
![]()
![]()
![]()
Como o campo elétrico é uniforme, temos que:
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 16
(UFLA-MG) As válvulas termiônicas, ainda hoje utilizadas em amplificadores de som "valvulados", podem ser constituídas por um cátodo e um ânodo. Os elétrons são emitidos pelo cátodo e acelerados em direção ao ânodo pelo campo elétrico uniforme gerado pela ddp aplicada aos eletrodos. Considere a massa do elétron igual a 9.10-31 kg, com carga de módulo igual a 1,6.10-19 C. A distância entre os eletrodos é de 1 cm e a ddp de 104 V. Calcule:
- O campo elétrico entre os eletrodos.
- A força elétrica que atua sobre os elétrons.
- A velocidade em que os elétrons estarão ao atingirem o ânodo, supondo que eles partiram do repouso.
Dados:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
Substituindo os valores:
![]()
![]()
O trabalho realizado pela força elétrica será equivalente à diferença entre a energia cinética final e a energia cinética inicial da partícula, uma vez que é o responsável por fornecer a energia necessária para o deslocamento:
![]()
Vale lembrar que a energia cinética é calculada pela seguinte fórmula:
![]()
Sabemos que a velocidade inicial será zero, pois os elétrons partem do repouso. Com isso, teremos:
![]()
![]()
![]()
![]()
![]()
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
POTENCIAL DE CONDUTOR EM EQUILÍBRIO ELETROSTÁTICO
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
Em um condutor em equilíbrio eletrostático, as cargas elétricas estão em movimento aleatório, sem qualquer deslocamento resultante ou concentração de carga elétrica em determinado ponto. Portanto, não há diferença de potencial elétrico entre dois pontos quaisquer desse condutor. Com isso, podemos concluir que um condutor em equilíbrio eletrostático possui o mesmo potencial elétrico em qualquer ponto. Denomina-se superfície equipotencial aquela na qual o potencial elétrico é constante em todos os seus pontos.
Uma superfície equipotencial possui linhas de força de campo elétrico perpendiculares à sua própria superfície (Figura 20).
Figura 20 - Linhas de força numa superfície equipotencial
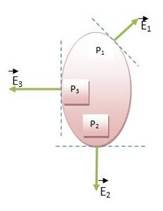
Fonte: Anjos (20--?) (https://brasilescola.uol.com.br/fisica/superficies-equipotenciais.htm)
No caso da Figura 20, VP1 = VP2 = VP3.
O campo criado por uma carga puntiforme irá gerar superfícies equipotenciais esféricas concêntricas, tendo a carga como centro (Figuras 21 e 22). Quanto mais próximo da carga, maior será o potencial elétrico da superfície esférica imaginária.
Figura 21 - Superfícies equipotenciais de carga puntiforme positiva
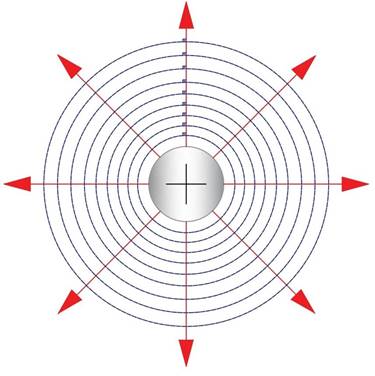
Fonte: Luiz Setti/Arquivo pessoal
Figura 22 - Superfícies equipotenciais de carga puntiforme negativa

Fonte: Luiz Setti/Arquivo pessoal
As superfícies equipotenciais são paralelas entre si em um campo elétrico uniforme, sendo perpendiculares às linhas de força do campo elétrico (Figura 23).
Figura 23 - Superfície equipotencial em um campo elétrico uniforme
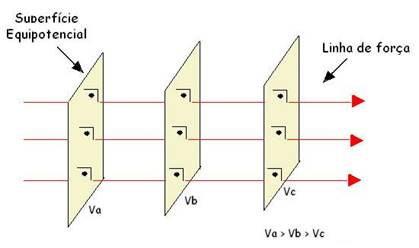
Fonte: Anjos (20--?) (https://brasilescola.uol.com.br/fisica/superficies-equipotenciais.htm)
EXERCÍCIO RESOLVIDO 17
Na Figura 24, são dadas as linhas de força de um campo elétrico uniforme e suas respectivas superfícies equipotenciais. Calcule:
- A intensidade do campo elétrico.
- O trabalho realizado pela força do campo para levar a carga q = –2 μC do ponto A até o ponto C.
- O potencial no ponto C.
Figura 24 - Exercício 17
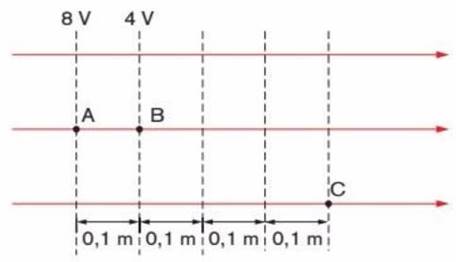
Fonte: Bonjorno et al. (2016)
Dados:
![]()
![]()
![]()
![]()
![]()
![]()
VA – VB = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ou
ou ![]()
![]()
Teremos:
![]()
![]()
![]()
![]()
EXERCÍCIO RESOLVIDO 18
A Figura 25 é a representação de duas cargas puntiformes X e Y e algumas de suas superfícies equipotenciais. As superfícies equipotenciais de X são representadas por linhas contínuas e as de Y, por linhas tracejadas. Quais são as polaridades de X e Y? E quais os valores dos potenciais em A, B, C e D?
Figura 25 - Exercício 18
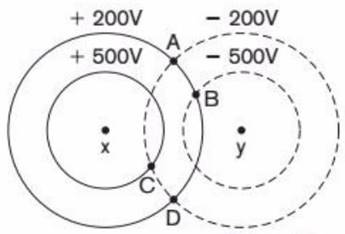
Fonte: Bonjorno et al. (2016)
Como os valores potenciais diminuem em valores positivos conforme aumenta distância das superfícies equipotenciais de X, essa carga tem sinal positivo.
Já Y, ocorre o oposto. Então o sinal dessa carga é negativo.
Assim: X é positivo e Y, negativo.
Para o segundo questionamento, sabemos que o potencial elétrico total em um ponto é a soma algébrica dos potenciais gerados pelas cargas elétricas que ali influem:
![]()
Portanto em A, levando em conta as superfícies equipotenciais em que está inserido este ponto:
![]()
![]()
Em B:
![]()
![]()
Em C:
![]()
![]()
Em D:
![]()
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
EXERCÍCIOS DE VESTIBULAR
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; FILHO, Luiz Antonio de Almeida. Conservação da Energia. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/ materias/conservacao-energia.html. Acesso em: [data de acesso].
1) (UF Santa Maria – RS) Considere a figura abaixo (Figura 26), na qual as linhas tracejadas representam superfícies equipotenciais devidas a duas placas carregadas com cargas de mesmo módulo e sinais contrários. Um elétron colocado no ponto P:
- Permanece em repouso.
- Desloca-se ao longo da linha, para cima.
- Desloca-se ao longo da linha, para baixo.
- Desloca-se perpendicularmente às linhas para a direita.
- Desloca-se perpendicularmente às linhas para a esquerda.
Figura 26 - Exercício de vestibular 1
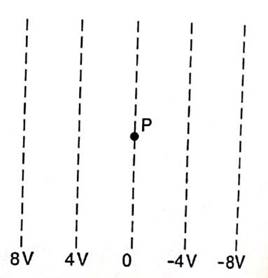
Fonte: Sampaio e Calçada (2000)
2) (USINA – SP) No campo elétrico criado no vácuo por uma carga Q puntiforme fica de 4,0.10-3 C é colocada uma carga q também puntiforme de 3,0.10-3 C a 20 cm da carga Q. A energia potencial adquirida pela carga q é:
- 6,0.10-3 J
- 8,0.10-2 J
- 6,3 J
- 5,4.105 J
3) (UEPG – PR) Seja V1 o potencial elétrico num ponto P situado a uma distância R de uma carga Q. Se reduzirmos à metade a distância R, o novo potencial elétrico V2 se relacionará com V1 da seguinte maneira:
- V2 = 2.V1
- V2 = V1/2
- V2 = V1
- V2 = 4.V1
- V2 = V1/4
4) (PUC – RS) Uma carga elétrica puntiforme Q>0 está colocada em um ponto P como mostra a figura abaixo. Os pontos que se encontram no mesmo potencial são:
Figura 27 - Exercício de vestibular 4
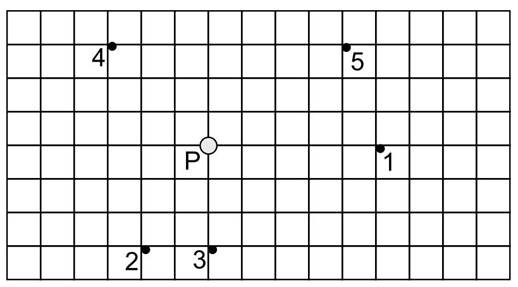
Fonte: PUC-RS
- 1 e 2.
- 1 e 5.
- 3 e 4.
- 1 e 4.
- 2 e 3
5) (VUNESP – SP) Para carregar uma bateria de 12 V, o carregador deve mover 4,5.105 C de carga do polo positivo para o polo negativo. Sendo o módulo da carga elementar do elétron e = 1,6.10-19 C, a quantidade de energia armazenada na bateria e o número de elétrons transferidos são, respectivamente:
- 7,2.106 J e 2,8.1024 elétrons.
- 5,4.106 J e 2,8.1024 elétrons.
- 5,4.106 J e 2,6.1024 elétrons.
- 2,7.106 J e 2,6.1024 elétrons.
- 1,9.106 J e 1,4.1024 elétrons.
6) (PUC-SP) Uma carga de 2,0.10-7 C encontra-se isolada, no vácuo, distante 6,0 cm de um ponto P. Qual a proposição correta?
- O vetor campo elétrico do ponto P está voltado para a carga.
- O campo elétrico no ponto P é nulo porque não nenhuma carga elétrica em P.
- O potencial elétrico no ponto P é positivo e vale 3,0.104 V.
- O potencial elétrico no ponto P é negativo e vale –5,0.104 V.
7) FUVEST – SP) São dadas duas cargas elétricas pontuais +Q e –Q de mesmo módulo, situadas como mostra a figura abaixo. Sabe-se que o potencial no ponto A vale 5,0 V, considerando-se nulo o potencial no infinito.
Determine o trabalho realizado pelo campo elétrico quando se desloca uma carga pontual q = 1,0 nC:
- do infinito até o ponto A;
- do ponto A até o ponto O.
FIGURA 28 - Exercício de vestibular 7
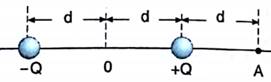
a) -5,0.10-9 J
b) 5,0.10-9 J
8) (FUVEST – SP) Um sistema formado por três cargas puntiformes iguais, colocadas em repouso nos vértices de um triângulo equilátero, tem energia potencial eletrostática igual a U. Substitui-se uma das cargas por outra, na mesma posição, mas com o dobro do valor. A energia potencial eletrostática do novo sistema será igual a:
- 4U/3
- 3U/2
- 5U/3
- 2U
- 3U
BIBLIOGRAFIA
BONJORNO, R. A.; BONJORNO, J. R.; BONJORNO, V.; RAMOS, C. M. Física. São Paulo: FTD, 1988.
BONJORNO, R. A.; BONJORNO, J. R.; BONJORNO, V.; RAMOS, C. M. Física fundamental. São Paulo: FTD, 2001.
BONJORNO, R. A.; BONJORNO, J. R.; BONJORNO, V.; RAMOS, C. M. Física 3: eletricidade. São Paulo: FTD, 1992.
BONJORNO, J. R.; BONJORNO, M. A.; BONJORNO, V.; RAMOS, C. M.; PRADO, E. P.; CASEMIRO, R. Física 3: eletromagnetismo e física moderna. São Paulo: FTD, 2016.
GONÇALVES FILHO, A.; TOSCANO, C. Física 3: interação e tecnologia. 2. ed. São Paulo: Leya, 2016.
RAMALHO JÚNIOR, F.; FERRARO, N. G.; SOARES, P. A. T. Os fundamentos da física. 10. ed. São Paulo: Moderna, 2009. (v. 3).
SAMPAIO, J. L.; CALÇADA, C. S. Física. São Paulo: Atual, 2005.
SAMPAIO, J. L.; CALÇADA, C. S. Física Clássica – Eletricidade. 2ª Edição. São Paulo: Atual, 2000.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021