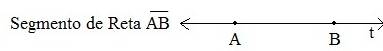Introdução à Geometria
IFSP - Cursinho Popular
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; MASCAI, Fabio Augusto Amaral; NASCIMENTO, Felipe Delgado do; SOARES, Matheus Ferreira. Introdução a Geometria. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/introducao-geometria.html. Acesso em: [data de acesso].
Tópicos: Introdução; Aplicações; Princípios; Ângulos; Quadriláteros.
Introdução: O assunto que veremos aqui é de fundamental importância para o seu sucesso! A geometria, em seus diversos conteúdos e abordagens, traz o conhecimento base para estudos posteriores, na aplicação em tantas outras áreas, garantindo também o sucesso no Exame Nacional do Ensino Médio (ENEM), onde grande parte das questões específicas envolviam os conceitos de geometria.
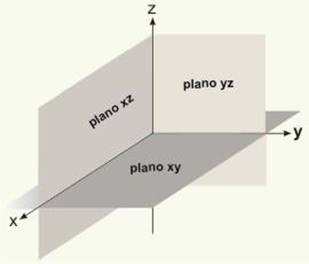
Por isso entende-se que ela é o ramo da matemática que estuda formas, tamanhos e posições na natureza, seja em padrões regulares de formação ou não. A geometria pode ser plana ou espacial, onde cada um desses elementos origina formas e metodologias de análise. Por essa razão é necessário analisar, interpretar e calcular as propriedades contidas nessa geometria
O material está dividido sequencialmente em aplicações, alguns conceitos primitivos e diversos exercícios de fixação. Não fique fora dessa e venha acompanhar a trilha do conhecimento em geometria!
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Aplicações
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; MASCAI, Fabio Augusto Amaral; NASCIMENTO, Felipe Delgado do; SOARES, Matheus Ferreira. Introdução a Geometria. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/introducao-geometria.html. Acesso em: [data de acesso].
Usos e Aplicações da Geometria
Ela está presente em tudo! Observe nas próximas imagens, as mais variadas formas de observarmos as formas geométricas na natureza, em obras construídas pelo homem etc.
Figura 1 – Exemplo de aplicação no trânsito

Fonte: Pixabay (2017) (https://pixabay.com/pt/photos/pilone-cone-do-tr%C3%A1fego-barreira-2915449/)
Além de sua beleza e funcionalidade, os cones de trânsito representam um sólido geométrico que possui algumas propriedades que serão abordadas posteriormente.
Agora veremos um exemplo natural de geometria.
Figura 2 – Hexágonos regulares em Colmeia

Fonte: Pixabay (2018) (https://pixabay.com/pt/photos/mel-colm%C3%A9ia-favo-de-mel-3216984/)
Observe o padrão de formação hexagonal, ou seja, seis lados exatamente iguais que estão arranjados naturalmente em larga escala, e que além de possibilitar um estudo profundo sobre geometria, traz o delicioso gosto de mel em nossas casas, não?
Figura 3 – Pirâmides do Egito

Fonte: Pixabay (2017) (https://pixabay.com/pt/photos/pir%C3%A2mides-egito-giz%C3%A9-arqueologia-2159286/)
Além de toda beleza magistral, essa maravilha do mundo deixa nítido o conhecimento de pirâmides, que intuitivamente conhecemos seu padrão de formação e aqui poderemos consolidar esses conceitos através de cálculos geométricos.
Figura 4 – Caixas e embalagens

Fonte: Pixabay (2020) (https://pixabay.com/pt/photos/cart%C3%A3o-embalagens-correio-pacote-5144898/)
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Princípios
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; MASCAI, Fabio Augusto Amaral; NASCIMENTO, Felipe Delgado do; SOARES, Matheus Ferreira. Introdução a Geometria. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/introducao-geometria.html. Acesso em: [data de acesso].
"A geometria está em tudo,
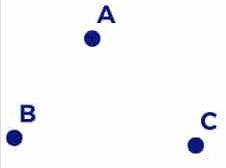
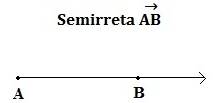
Ela surge do nada, forma pontos, retas, semirretas, segmentos
A beleza se origina nessa união implacável!
Com suas formas, lados e ângulos
Moldamos tudo o que vemos no cotidiano
Como quadrados e triângulos
Tudo tem sua área, volume, suas propriedades"
O texto acima nos mostra o princípio do nosso estudo, leia com calma atente-se aos termos utilizados. Não se preocupe em entendê-los agora, pois caminharemos juntos por todos os elementos da geometria. Apresentaremos tudo, do começo até o fim.
Primeiros Conceitos de Geometria e Organograma com a Formação Lógica do Assunto
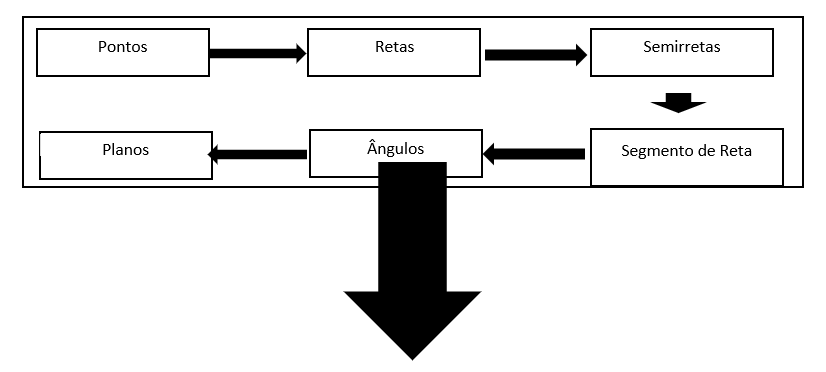
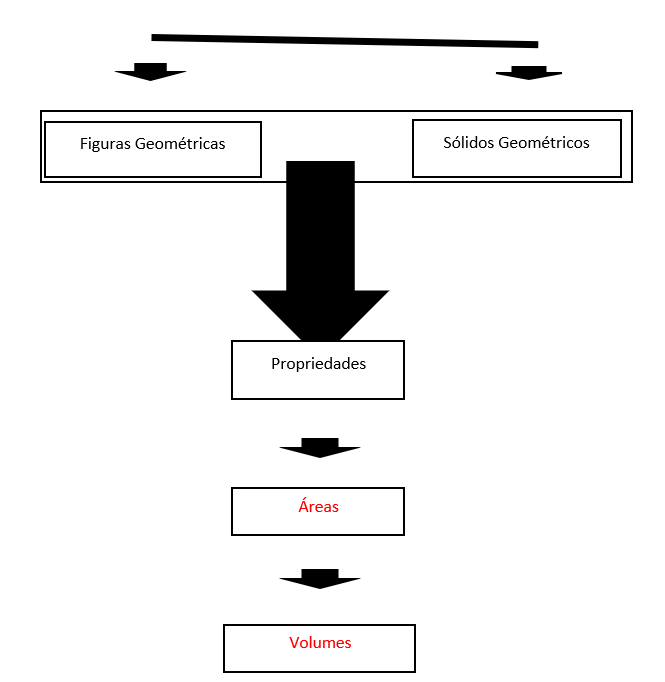
Aqui você encontrará a visão esquemática de todo o estudo da geometria, o seu conhecimento é ilimitado e como vimos, ele possui diversas aplicações em toda sua vida. Com isso, apresentaremos os principais tópicos e suas origens, facilitando maior entendimento do contexto.
Sempre que precisar, retorne nessa página e revise o organograma do assunto, assim como após qualquer conteúdo abordado, você também regresse aqui e localize onde aquele conhecimento deve ser alocado. Aprecie sem moderação!!
Clique nos Blocos para mais informações:
...
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Quadriláteros
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; MASCAI, Fabio Augusto Amaral; NASCIMENTO, Felipe Delgado do; SOARES, Matheus Ferreira. Introdução a Geometria. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/introducao-geometria.html. Acesso em: [data de acesso].
Introdução às figuras: Quadriláteros
Assim como a combinação da palavra polígono (poli + gono), temos nomenclatura parecida, onde o termo quadrilátero é expresso por:
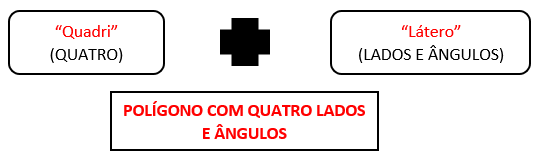
Mas inicialmente, vale ressaltar que, assim como o quadrilátero, um polígono pode possuir 5, 6 ou vários lados com seus respectivos ângulos, a tabela a seguir apresenta alguns modelos e sua relação de lados.
Tabela 1 – Relação de polígonos e quantidade de lados
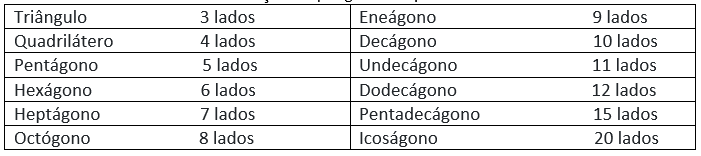
Não se preocupe com a quantidade de elementos, conheceremos os essenciais, aumentando a complexidade conforme o andamento do conteúdo.
Tratando-se dessas definições, veremos o primeiro exemplo de quadrilátero, o famoso quadrado.
Figura 20 – Quadrado
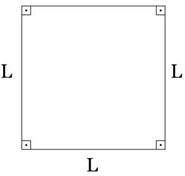
Fonte: Educa mais Brasil (2019) (https://www.educamaisbrasil.com.br/enem/matematica/area-do-quadrado).
Como o próprio nome já diz, ele possui quatro lados iguais, além disso, possui uma diagonal principal, assim como a soma dos seus ângulos internos que formam um total de 360°.
Como demonstrado na figura do quadrado, as quatro medidas são de tamanhos iguais, chamadas de L. A partir disso, partiremos para o próximo quadrilátero bastante utilizado também.
Retângulo
Como vimos no exemplo do quadrado, o retângulo também possui a soma de ângulos igual a 360°, porém as medidas dos lados são diferentes! Observe.
Figura 22 – Retângulo

Fonte: Ferreto (2019) (https://blog.professorferretto.com.br/retangulo/).
Figura 23 – Lados do retângulo

Fonte: Ferreto (2019) (https://blog.professorferretto.com.br/retangulo/).
Observe que estamos considerando uma medida a e a outra b, mas pode ser chamado também de base e altura.
Derivação do Retângulo: Paralelogramo
Para entendermos as derivações até o momento, iremos sintetizar as etapas de evolução entre esses polígonos:
- Do quadrado para o retângulo: mudança nas medidas dos lados.
- Do retângulo para o paralelogramo: mudança nas medidas dos ângulos.
Para comprovar os dois tópicos elencados, observe a formação do paralelogramo a seguir.
Figura 24 – Paralelogramo

Fonte: Ferreto (2019) (https://blog.professorferretto.com.br/retangulo/).
Figura 25 – Lados do paralelogramo

Fonte: Ferreto (2019) (https://blog.professorferretto.com.br/retangulo/).
...
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021