Geometria plana – área e perímetro
IFSP - Cursinho Popular
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
Tópicos: Introdução; Aplicações; Conceitos iniciais; Fórmulas; Exercícios propostos
Introdução: O assunto área e perímetro é de suma importância para o aprendizado da geometria plana, isso devido ao fato de esses conceitos atuarem como a base da geometria. Estando em grande parte das questões do Exame Nacional do Ensino Médio (ENEM), entender como funciona e como aplicar as fórmulas é necessário para garantir uma ótima pontuação.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Uso e Aplicações
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
No decorrer do dia a dia é possível observar o uso da área e do perímetro em tudo, como nas imagens a seguir.
Figura 01 – Exemplo de aplicação na escola

Fonte: Pixabay (https://pixabay.com/pt/illustrations/educa%C3%A7%C3%A3o-volta-%C3%A0s-aulas-1545578/)
Os desenhos demarcados com linhas pretas, são exemplos típicos de áreas, sendo a lousa ("Back to school" – De volta à escola), o globo terrestre e o esquadro, representantes das figuras geométricas retangular, circular e triangular, respectivamente.
Outro exemplo marcante pode ser encontrado na prática do futebol, pois traz consigo diversas regras, sendo uma delas as demarcações de dimensões corretas, observe na imagem abaixo.
Figura 02 – Campo de futebol
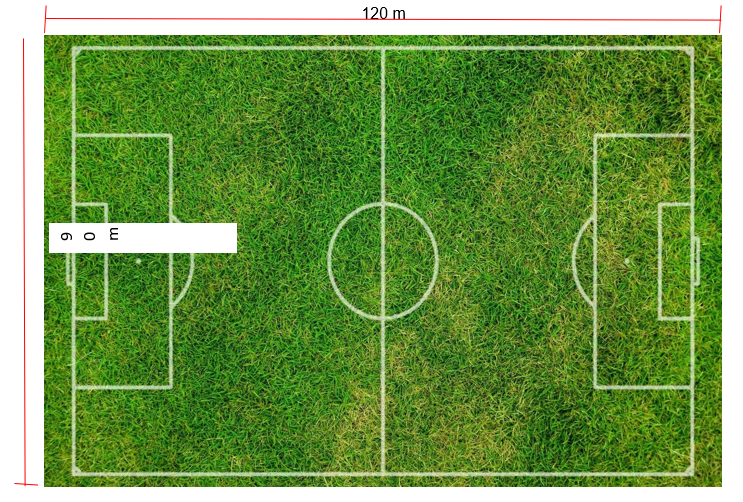
Fonte: Pixabay (2014) (https://pixabay.com/pt/photos/campo-de-futebol-futebol-rush-320100/)
Observe que o campo de futebol representa a forma geométrica de um retângulo, pois é um quadrilátero com todos os seus ângulos medindo 90º. Viu só? O dia a dia guarda uma infinidade de formas geométricas que as vezes passam sem que percebamos. A partir dessas aplicações é possível demostrarmos os diversos conceitos existentes.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Conceitos iniciais
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
O estudo das formas geométricas se dá primeiramente na geometria plana, onde tem-se que os pontos, retas e polígonos de uma figura pertencem a um mesmo plano.
Além desses relevantes assuntos, é de extrema importância a definição de dois conceitos: base e altura. De modo a explicarmos sobre os conceitos, tomemos como exemplo a figura de um retângulo. Observe o exemplo abaixo.
Figura 03 – Retângulo
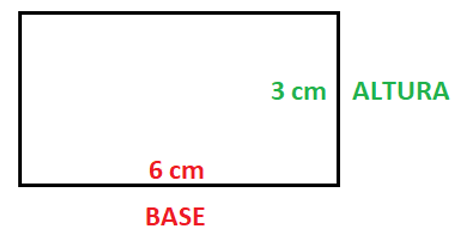
Fonte: Acervo pessoal
Na figura anterior, tem-se um retângulo, onde foi indicado sua base e altura.
Em vermelho tem-se a base, ou seja, o lado em que será tomado como referência. Essa figura possui lados opostos, congruentes e paralelos entre si. Já em verde há a indicação da altura que a figura possui, ou seja, a distância entre as bases.
De acordo com os dados do exemplo, a base possui um valor de 6 cm enquanto a altura é 3 cm. A partir dessas informações é possível calcular tanto a área, quanto o perímetro dessa figura.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
O que é área e perímetro?
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
Acerca dos conceitos estudados anteriormente, pode-se concluir que a área equivale ao espaço total que uma superfície ocupa em determinado plano e tem como unidade de medida cm² (centímetros quadrados), m² (metros quadrados), km² (quilómetros quadrados), entre outros. Observe a imagem abaixo.
Figura 04 – Casa vista de cima
Fonte: Freepik (2016) (https://br.freepik.com/vetores-gratis/desenho-vista-interior-de-uma-casa_1047895.htm)
Figura 05 – Piso

Fonte: Pixabay (2018) (https://pixabay.com/pt/photos/modelo-telha-piso-3097484/)
Imaginemos que as figuras acima representem os cômodos de uma casa que estão passando por uma reforma e o piso que será utilizado para decoração, respectivamente. Os construtores precisam saber quantos pisos serão colocados em um dos quartos e para isso precisam calcular a área de cada um dos pisos. Cada figura geométrica possui uma maneira diferente de se calcular sua área. Esses pisos, possuem o formato de um quadrado.
Um quadrado possui quatro lados iguais e partindo do princípio de que a área é calculada a partir da fórmula:
![]()
Temos que a área do quadrado será calculada aplicando a seguinte fórmula:
![]()
Diferentemente da área, o perímetro calcula o contorno das figuras, a partir do somatório das medidas que o formam, ou seja, o comprimento da figura e possui como unidade de medida o cm (centímetro), m (metro), km (quilômetros), entre outros. Para exemplificar o conceito, observe a imagem abaixo.
Figura 06 – Figuras geométricas
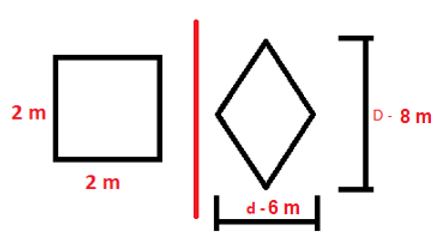
Fonte: Acervo pessoal
Ao lado esquerdo da figura encontra-se um quadrado que possui como medida lateral 2 m, se aplicarmos o conceito de perímetro, encontraremos que:
![]()
Seguindo o contorno da figura (linha preta), tem se que, ao fazer o somatório da medida de cada lado, o perímetro encontrado equivale a 8 m.
A figura geométrica do lado direito é conhecida como losango e seus lados medem 5 m, por exemplo. Portanto, seu perímetro será:
![]()
Para encontrar a área de um losango usa se a fórmula:
![]()
Onde:
D – diagonal maior
d – diagonal menor
Figura 07 – Figuras geométricas – demonstração de fórmulas
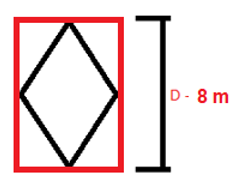
Fonte: Acervo pessoal
Na imagem acima, tem-se um losango inserido em um retângulo, mas a que conclusões podemos chegar ao estudar a imagem?
A fórmula do losango diz que sua área é dada por:
![]()
Se retornamos a imagem agora, podemos perceber que a diagonal maior do losango equivale a altura do retângulo e o mesmo ocorre quando comparamos a diagonal menor do losango com a base do retângulo.
Mas, porque, então as fórmulas usadas são diferentes? Enquanto a fórmula do losango tem seu resultado dividido por dois, o retângulo, não.
Isso é devido ao fato de a área do losango equivaler à metade da área do retângulo. Observe os cálculos a seguir.
![]()
![]()
A partir da resolução utilizando ambas as fórmulas, observa-se que os resultados foram iguais, mas para isso foi necessário dividir a área do losango por dois.
E aí, já havia parado para pensar nisso?
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Fórmulas
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
Após entendidos os conceitos de área e perímetro, é importante estudarmos as fórmulas da área para cada figura geométrica em particular.
Já foi visto que a fórmula da área do quadrado é ![]() e a do losango é
e a do losango é ![]() , porém e as outras fórmulas? Observe as imagens abaixo.
, porém e as outras fórmulas? Observe as imagens abaixo.
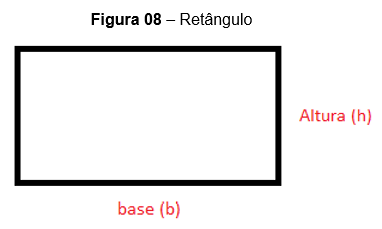
Fonte: Acervo pessoal
O cálculo da área do retângulo, como já vimos, é dado pela fórmula
![]()
Enquanto o perímetro é encontrado por meio da fórmula:
![]()
![]()
Figura 09 – Triângulo
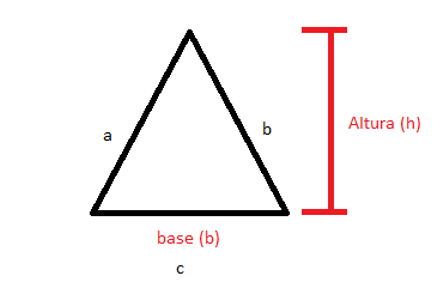
Fonte: Acervo pessoal
Para calcular a área do triângulo, aplica se a fórmula abaixo:
![]()
E seu perímetro pode ser calculado a partir da soma de seus lados:
![]()
Existem diversos tipos de triângulos, um deles é o triângulo obtuso. Observe a imagem e o exemplo abaixo.
Figura 10 – Triângulo obtusângulo
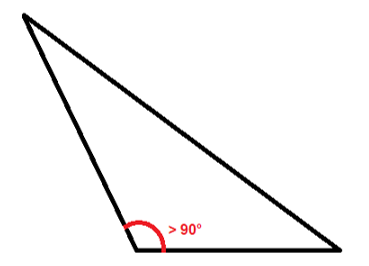
Fonte: Acervo pessoal
A partir da imagem acima e da fórmula vista anteriormente, calcule a área de um triângulo obtusângulo que possui uma base de 20 cm e uma altura de 40 cm.
![]()
Do mesmo modo do losango, vamos pensar um pouco mais a fundo sobre a fórmula da área de um triângulo? Para isso, observe a imagem abaixo.
Figura 11 – Triângulo – demonstração de fórmulas

Fonte: Acervo pessoal
Na imagem acima, foi inserido um triângulo em um retângulo de modo a pensarmos na origem da fórmula da figura de três lados.
A fórmula do triângulo diz que sua área é dada por:
![]()
Se relembrarmos a fórmula do retângulo, tem-se que ela equivale a
![]()
Ao compararmos ambas as fórmulas descobrimos que elas possuem uma parte equivalente. Mas, então, por que a fórmula da área do triângulo possui uma divisão por dois?
Isso é devido ao fato de que a área do triângulo equivaler à metade da área do retângulo.
Figura 12 – Círculo
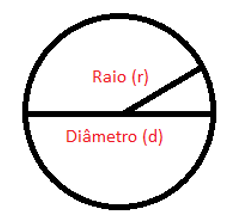
Fonte: Acervo pessoal
Pode-se calcular a área de duas diferentes fórmulas, veja-as abaixo:
![]()
![]()
Diferentemente do modo em que se calcula o perímetro nas figuras geométricas anteriores, o perímetro do círculo é também conhecido como circunferência e pode ser encontrado pela fórmula abaixo.
![]()
Figura 13 – Trapézio
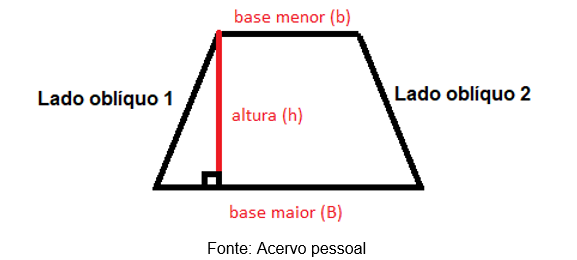
Para encontrar a área do trapézio é usada a fórmula abaixo:
![]()
Enquanto o perímetro será a soma de seus lados, observe a fórmula abaixo:
![]()
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios propostos
Como citar este documento: CAMPOS, Ayumi Kato; Cruz, Paulo Henrique Correia Araújo da; OLIVEIRA, Ana Carolina Machado de. Geometria Plana – Área E Perímetro. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-plana-area-e-perimetro.html. Acesso em: [data de acesso].
1) (ENEM – 2015) O prefeito de uma cidade deseja promover uma festa popular no parque municipal para comemorar o aniversário de fundação do município. Sabe-se que esse parque possui formato retangular, com 120 m de comprimento por 150 m de largura. Além disso, para a segurança das pessoas presentes no local, a polícia recomenda que a densidade média, num evento dessa natureza, não supere quatro pessoas por metro quadrado.
Seguindo as recomendações de segurança estabelecidas pela polícia, qual é o número máximo de pessoas que poderão estar presentes na festa.
- 1 000.
- 4 500.
- 18 000.
- 72 000.
- 120 000.
- Como são 4 pessoas por metro quadrado, a cada m² temos 4 pessoas, assim, sendo P o número máximo de pessoas:
![]()
Letra D
2) (Enem - 2015) O esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.
Figura 1
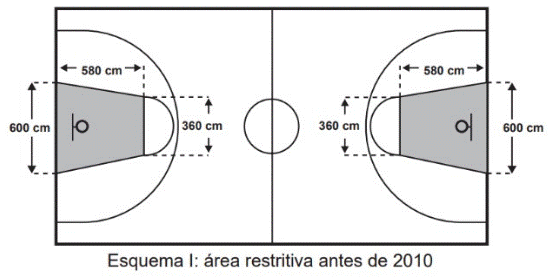
Fonte: Só exercício (2015) (https://soexercicios.com.br/plataforma/questoes-de-vestibular/ENEM/55608-55609/-area-do-retangulo-b-area-do-quadrado-b-rec-/1)
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diferentes ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
Figura 2
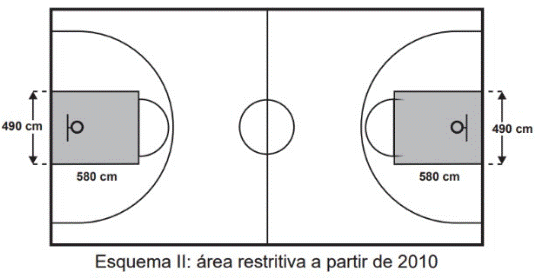
Fonte: Só exercício (2015) (https://soexercicios.com.br/plataforma/questoes-de-vestibular/ENEM/55608-55609/-area-do-retangulo-b-area-do-quadrado-b-rec-/1)
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
a) aumento de 5 800 cm2.
b) aumento de 75 400 cm2.
c) aumento de 214 600 cm2.
d) diminuição de 63 800 cm2.
e) diminuição de 272 600 cm2.
- Comecemos pela área do trapézio da figura I, que é dada por:
![]()
Calculando a área da figura II temos:
![]()
Assim, o aumento da área foi de 5 800 cm².
Letra A
3) (ENEM – 2017) A figura traz o esboço da planta baixa de uma residência. Algumas medidas internas dos cômodos estão indicadas. A espessura de cada parede externa da casa é 0,20 m e das paredes internas 0,10 m.
Figura 1
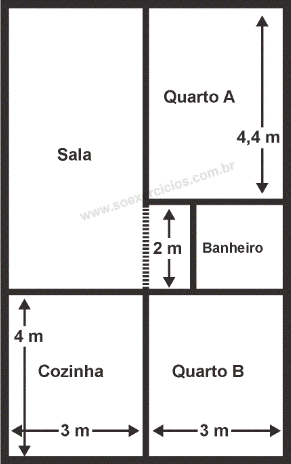
Fonte: Só exercício (2017) (https://soexercicios.com.br/plataforma/questoes-de-vestibular/ENEM/55608-55609/-area-do-retangulo-b-area-do-quadrado-b-rec-/1)
Sabe-se que, na localidade onde se encontra esse imóvel, o Imposto Predial Territorial Urbano (IPTU) é calculado conforme a área construída da residência. Nesse cálculo, são cobrados R$ 4,00 por cada metro quadrado de área construída.
O valor do IPTU desse imóvel, em real, é
- 250,00.
- 250,80.
- 258,64.
- 276,48.
- 286,00.
- Sendo
![]()
![]()
Logo o valor será:
![]()
Letra E
4) Para garantir a segurança de um grande evento público que terá início às 4h da tarde um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2 000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120 000 pessoas por hora até o início do evento quando não será mais permitida a entrada de público.
Quantos policiais serão necessários no início do evento para garantir a segurança?
- 360.
- 485.
- 560.
- 740.
- 860.
- Como a área do evento é de 500² m² e a cada m² cabem 4 pessoas, às 10 horas da manhã haviam
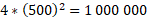 de pessoas presentes e até as 4 horas da tarde chegarão mais
de pessoas presentes e até as 4 horas da tarde chegarão mais 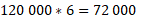 pessoas.
pessoas.
Assim serão necessários
![]()
Letra E
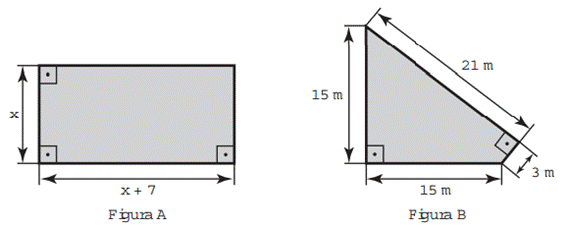
5) (ENEM – 2016) Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.
Figura 1
Fonte: Descomplica (2016) (https://descomplica.com.br/gabarito-enem/questoes/2016/segundo-dia/um-senhor-pai-de-dois-filhos-deseja-comprar-dois-terrenos/)
Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a:
- 7,5 e 14,5.
- 9,0 e 16,0.
- 9,3 e 16,3.
- 10,0 e 17,0.
- 13,5 e 20,5.
- Primeiramente, dividimos a figura B em dois triângulos B1 e B2, um com altura de 21 m e base de 3 m e outro com altura e base medindo 15 m.
Assim, temos que área da figura A = área da figura B = B1 + B2
![]()
Fatorando 144, temos que:
![]()
![]()
Assim, as medidas do retângulo são 9 m e 16 m.
Letra B
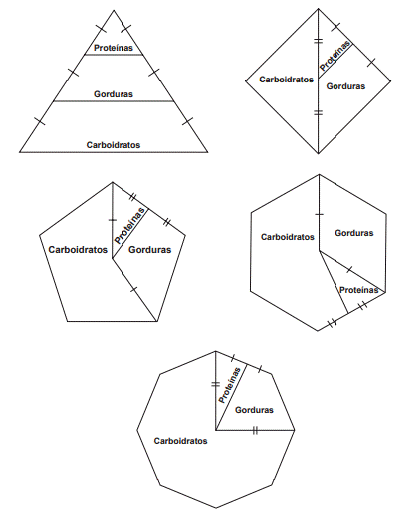
6) Para uma alimentação saudável, recomenda-se ingerir, em relação ao total de calorias diários, 60% de carboidratos, 10% de proteínas e 30% de gorduras. Uma nutricionista, para melhorar a visualização dessas porcentagens, quer dispor esses dados em um polígono. Ela pode fazer isso em um triângulo equilátero, um losango, um pentágono regular, um hexágono regular ou um octógono regular, desde que o polígono seja dividido em regiões cujas áreas sejam proporcionais às porcentagens mencionadas.
Ela desenhou as seguintes figuras:
Figura 1
Fonte: Descomplica (2015): (https://descomplica.com.br/gabarito-enem/questoes/2015/segundo-dia/para-uma-alimentacao-saudavel-recomenda-se-ingerir-em-relacao-ao-total-de-calorias-diaria/)
Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o
- Triângulo.
- Losango.
- Pentágono.
- Hexágono.
- Octógono.
- Estes são todos derivados de gráficos de pizza e, algumas análises podemos fazer parecidas. Analisando o gráfico em forma pentagonal, podemos pensar que, partindo do centro, os 360°, ou os 100%, são repartidos em 5 partes. Então cada lado do pentágono ficou com 20%.
Então, como os carboidratos ficaram com 3 lados do pentágono,
![]()
As proteínas ficaram com metade de um lado
![]()
e a gordura ficou com o resto que faltava para
![]()
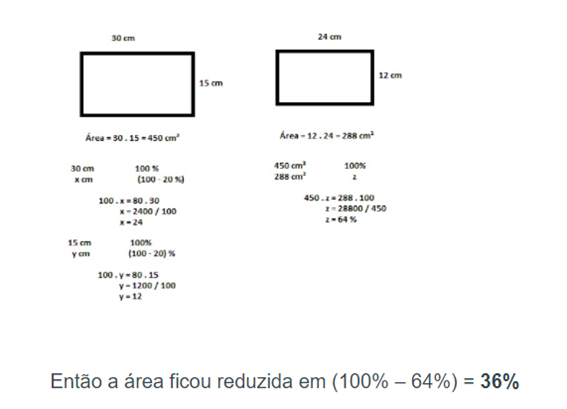
7) (ENEM – 2013) A cerâmica constitui-se em um artefato bastante presente na história da humanidade. Uma de suas várias propriedades é a retração (contração), que consiste na evaporação da água existente em um conjunto ou bloco cerâmico quando submetido a uma determinada temperatura elevada. Essa elevação de temperatura, que ocorre durante o processo de cozimento, causa uma redução de até 20% nas dimensões lineares de uma peça.
Suponha que uma peça, quando moldada em argila, possuía uma base retangular cujos lados mediam 30 cm e 15 cm. Após o cozimento, esses lados foram reduzidos em 20%.
- 4%.
- 20%.
- 36%.
- 64%.
- 96%.
Letra C
8) Um carpinteiro fabrica portas retângulas maciças, feitas de um mesmo material. Por ter recebido de seus clientes pedidos de portas mais altas, aumentou sua altura em 1/8 preservando usas espessuras. A fim de manter o custo com o material de cada porta, precisou reduzir a largura.
A razão entre a largura da nova porta e a largura da porta anterior é:
- 1/8.
- 7/8.
- 8/7.
- 8/9.
- 9/8.
- Temos que a nova altura da porta será de:
![]()
Essas portas terão o mesmo custo se tiverem a mesma área da superfície, assim, temos:
![]()
![]()
![]()
Assim, a razão entre as larguras será:
![]()
Letra D
9) (ENEM 2013) Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas. Devido a uma demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada. A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:
- N/9.
- N/6.
- N/3.
- 3/N.
- 9/N.
Antes:
![]()
![]()
![]()
![]()
![]()
![]()
Depois:
![]()
![]()
![]()
![]()
Alternativa A
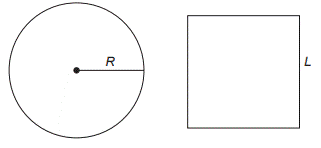
10) (ENEM 2020 - PPL) Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L.
Figura 1
Fonte: Concursos (2021) (https://www.qconcursos.com/questoes-do-enem/disciplinas/matematica-matematica/areas-e-perimetros/questoes)
A fórmula correta é:
- R = L / √π.
- R = L/ √2π.
- R = L²/ 2π.
- R = √2 L/ π.
- R = 2 *
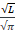 .
.
Iguala-se as áreas e isola-se o R:
![]()
![]()
![]()
Alternativa A
11) (ENEM 2020 – PPL) Projetado pelo arquiteto Oscar Niemeyer, o Museu de Arte Contemporânea (MAC) tornou-se um dos cartões-postais da cidade de Niterói (Figura 1).
Figura 1

Fonte: (https://download.inep.gov.br/enem/provas_e_gabaritos/2020_PV_reaplicacao_PPL_D2_CD7.pdf)
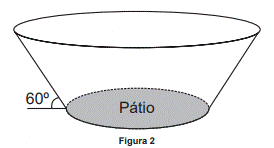
Considere que a forma da cúpula do MAC seja a de um tronco de cone circular reto (Figura 2), cujo diâmetro da base maior mede 50 m e 12 m é a distância entre as duas bases. A administração do museu deseja fazer uma reforma revitalizando o piso de seu pátio e, para isso, precisa estimar a sua área. (Utilize 1,7 como valor aproximado para 3 e 3 para π).
Figura 2
Fonte: (https://download.inep.gov.br/enem/provas_e_gabaritos/2020_PV_reaplicacao_PPL_D2_CD7.pdf)
A medida da área do pátio do museu a ser revitalizada, em metro quadrado, está no intervalo
- [100, 200].
- [300, 400].
- [600, 700].
- [900. 1 000].
- [1 000, 1 100].
Usa-se as relações trigonométricas no triângulo retângulo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A área do piso do pátio é a circunferência de raio R.
![]()
![]()
![]()
![]()
Alternativa D
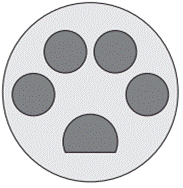
12) (ENEM 2020 – PPL) Para identificar visualmente uma loja de pet shop, um empresário criou uma logomarca que se assemelha a uma marca deixada pela pegada de um gato, como na figura. O maior círculo tem medida de raio igual a 6 cm. O empresário pretende reproduzir o desenho em uma das paredes retangulares da loja. Para isso, fará a ampliação da logomarca utilizando a escala de 1:25.
Figura 1
Fonte: (https://download.inep.gov.br/enem/provas _e_gabaritos/2020_PV_reaplicacao_PPL_D2_CD7.pdf)
A área mínima, em metro quadrado, que a parede deverá ter para que a logomarca seja aplicada é:
- 2,25
- 6,00
- 7,06
- 9,00
- 36,00
Primeiramente é preciso obter o tamanho real do desenho e para isso faz se a conversão na escala de 1:25.
![]()
![]()
![]()
Como as alternativas estão em m² é preciso converter:
![]()
A área de uma circunferência é calculada por:
![]()
Como o enunciado não traz o valor de ![]() , adotaremos como 3,14:
, adotaremos como 3,14:
![]()
Alternativa D
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021