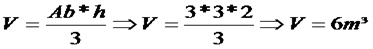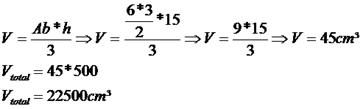Geometria Espacial – Volume
IFSP - Cursinho Popular
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Introdução: O assunto volume é de suma importância para o aprendizado da geometria espacial, isso devido ao fato de esses conceitos atuarem como a base da geometria. Estando em grande parte das questões do Exame Nacional do Ensino Médio (ENEM), entender como funciona e como aplicar as fórmulas é necessário para garantir uma ótima pontuação.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Uso e Aplicações
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Em nosso cotidiano podemos observar o volume em diversos materiais, objetos, estruturas, entre outras coisas, como demonstra as imagens abaixo.
Figuras 1, 2 e 3 - Aplicações do Volume no Cotidiano

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Mas afinal o que seria Volume?!
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Volume é a medida do espaço ocupado por um sólido, por um líquido ou por um gás.
As unidades de medidas para o Volume são padronizadas. Veja no quadro a seguir!
Tabela 1 - Unidades de Volume
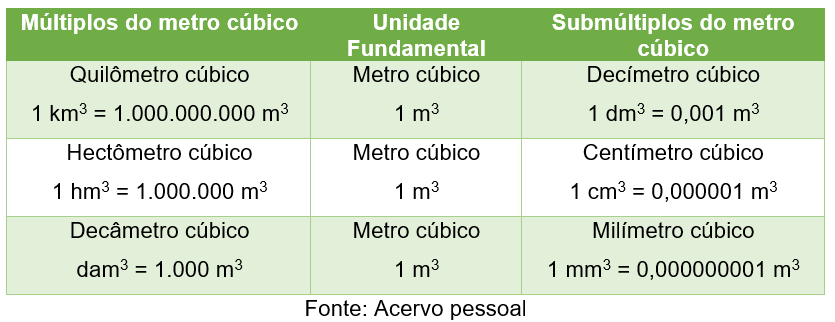
Mas fique tranquilo, as unidades mais utilizadas para expressar volumes, são o metro cúbico, decímetro cúbico e o centímetro cúbico
Para a conversão das Unidades de Medida utilizamos a regra de conversão abaixo:
Tabela 2 - Conversão de Unidades de medidas de Volume

Vamos praticar!
Exemplo: Quantos centímetros cúbicos há em 1/2 metros cúbicos.
Como da direita para a esquerda cada unidade representa 1000 vezes a unidade seguinte, multiplicamos 1/2 por 1000 X 1000 (1 000 000).
1/2 metros cúbicos = 0,5 metros cúbicos= (0,5 X 1 000 000) centímetros cúbicos
= 500 000 centímetros cúbicos
Exercícios de Fixação
1- Uma lata de tinta possui um volume de 26 dm3. Qual o volume desta lata em metros cúbicos?
- Milímetro cúbico (mm3)| centímetro cúbico(cm3) | decímetro cúbico (dm3) | metro cúbico (m3) | decâmetro cúbico (dam3) | hectômetro cúbico (hm3) | quilômetro cúbico (km3)
- De decímetro cúbico (dm3) para metro cúbico (m3), dividimos por 1000, então devemos andar três casas para a esquerda no número 26 dm3, ou seja, 26,0 dm3, se tornará 0,026 m3.
2- Transforme 8 km3 em m3.
3- Transforme 10 mm3 em dam3.
- 1 × 10^-11 decâmetro cubo.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Você sabe qual a diferença entre Volume e Capacidade?
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Muitos podem acabar confundindo Volume e Capacidade, pois apesar de serem conceitos próximos são diferentes. Volume seria o "espaço" que o objeto ocupa. A capacidade seria o quanto o objeto é capaz de transportar, ou seja, capacidade seria o volume "interno" do objeto.
As medidas de capacidade mais utilizadas são o litro (L), o decilitro (dL) e o centilitro (cL).
Observe o quadro abaixo:
Tabela 3 - Quadro de Unidades de medidas de Capacidade
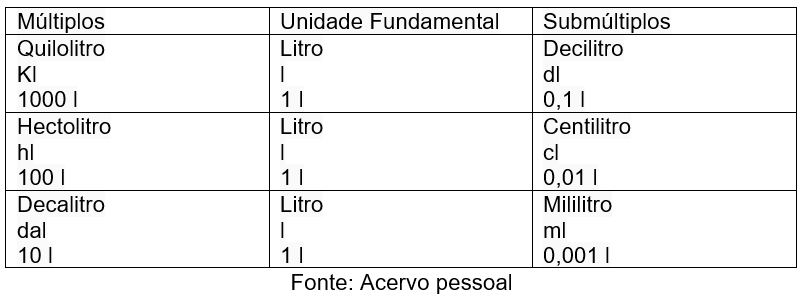
Para a conversão das Unidades de Medida utilizamos a regra de conversão abaixo:
Tabela 4 - Conversão de Unidades de Capacidade

Vamos praticar!
Exemplo I: Expressar 15 L em mililitros.Exemplo II: Expressar 330 mL em litros.
Exercícios de Fixação
4- Quantos litros cabem em uma lata de 35 cl.
5- Expresse 1 hl, 3.5 dl e 87 ml em litros.
6- Para tirar água de um poço, você possuiu apenas dois baldes: um de 5 litros e um de 3. Você precisa ficar, exatamente, com 1 litro de água. O que você faria?
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Volume de Prismas Retos
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Ao estudar Volume vem em mente diversos sólidos geométricos:
Figura 4 - Sólidos Geométricos

Fonte: Pixabay (https://cdn.pixabay.com/photo/2016/10/ 16/01/18/colors-1744138__340.jpg)
Vamos iniciar nosso estudo trabalhando o Volume de Prismas Retos que é uma forma de mensurar a quantidade de espaço ocupada por eles a partir de algumas de suas medidas.
Volume de Prismas Retos
Os primas são sólidos do grupo dos poliedros, aqueles que têm apenas superfícies planas. O prisma reto é caracterizado por duas faces paralelas iguais, que são suas bases e as outras faces formadas por retângulos, sendo suas faces laterais. Veja alguns exemplos abaixo.- Bloco retangular (Paralelepípedo) e cubo:
De modo prático, sabemos que é possível calcular o volume de um bloco retangular multiplicando suas três dimensões.
Figura 5 - Paralelepípedo
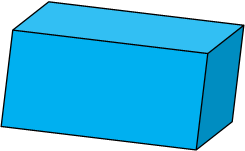
Fonte: Acervo pessoal
Sendo: Volume= Área da base (comprimento . largura) . altura ![]() V= Ab.a
V= Ab.a
Vamos analisar, agora, o caso do cubo: ele é um bloco retangular em que o comprimento, a largura e a altura têm medidas iguais. Dessa forma temos a seguinte relação:
Figura 6 - Cubo
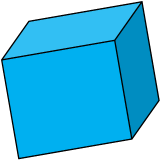
Fonte: Acervo pessoal
Sendo: c=l=a, ou seja lados com medidas iguais, temos L ao cubo, pois são três dimensões.
Volume=Área da base (a.a) . a= Lado 3 ![]() V= L3
V= L3
Com isso percebemos de modo geral, que o cálculo do Volume de um prisma seria:
V prisma = área da base . altura
Podemos então calcular o volume de diversos prismas retos sabendo calcular a área das figuras dos mesmos.
Vamos praticar!
Exemplo: Um bloco retangular possui 17 cm de largura, 10 cm de comprimento e 45 cm de altura. Qual é o volume desse bloco retangular?
Assim volume do prisma será calculado da seguinte forma:
V = AB·h V = 170·45 V = 7650 cm3
Exercícios de Fixação
7- (UE-CE) Com 42 cubos de 1 cm de aresta formamos um paralelepípedo cujo perímetro da base é 18 cm. A altura deste paralelepípedo, em cm, é:
Perímetro:
x + x + y + y = 18
2x + 2y = 18 -> simplificando por 2 ---> x + y = 9
Área da base --> x.y
Volume do paralelepípedo . Cada cubo tem 1cm³ de volume (logo o paralelepípedo tem 42 cm³ de volume)
V = xy * h
42 = xy * h
h = 42/xy
Possibilidades para x e y e para área da base
x + y = 9 -----> área da base xy
1 + 8 ------ > 1 * 8 = 8
2 + 7 ---------> 2 * 7 = 14
3 + 6 ---------> 3 * 6 = 18
4 + 5 --------> 4 * 5 = 20
A divisão 42/xy deve ser um numero inteiro
por 8 , 18 e 20 não daria n° inteiro
A única possibilidade pra xy é 14
h = 42/14
h = 3
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios do Enem
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
1)(Enem – 2017) Um empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugere que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d'água dessa piscina é mantido a 50 cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é:
a) 11,25.
b) 27,00.
c) 28,80.
d) 32,25.
e) 49,50
- Primeiro precisamos descobrir o volume da nossa piscina, considerando que a piscina só é cheia até 50 cm da borda, vamos considerar a altura:
1,70 - 50 = 1,20 m .
Para sabermos o volume do nossa piscina retangular vamos fazer:
V = Altura x comprimento x largura
V = 1,20 x 5 x 3
V = 18 m3
Também sabemos que 1000 L equivalem a 1 m3.
Então precisamos de 1,5 ml do produto por m3, e sabemos que temos 18 m3 de água,
Então= 18 * 1,5 = 27 Ml. Vamos precisar de 27 ml do produto,
Alternativa: B 27,00
2)(Enem – 2017) Em alguns países anglo-saxões, a unidade de volume utilizada para indicar o conteúdo de alguns recipientes é a onça fluida britânica. O volume de uma onça fluida britânica corresponde a 28,4130625 mL.
A título de simplificação, considere uma onça fluida britânica correspondendo a 28 mL.
Nessas condições, o volume de um recipiente com capacidade de 400 onças fluidas britânicas, em cm3, é igual a:
a) 11 200.
b) 1 120.
c) 112.
d) 11,2.
e) 1,12.
- 1 cm3 = 1 ml
1 onça —— 28 cm3
400 onças — x
Alternativa: A 11.200
3(Enem 2011) Um mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro sejam obtidas em metros: a) distância a entre os eixos dianteiro e traseiro;
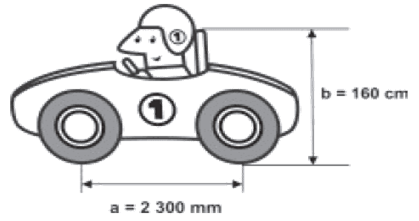
Ao optar pelas medidas a e b em metros, obtêm-se, respectivamente,
a)0,23 e 0,16
b) 2,3 e 1,6
c) 23 e 16
d) 230 e 160
e) 2.300 e 1.600
- Precisamos fazer a conversão de unidades.
Sabemos que:
1 m = 1 000 mm
1 m = 100 cm
Alternativa: B 2,3 e 1,6
4)(Enem 2010) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura. Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a:
A) 5 cm
B) 6 cm
C) 12 cm.
D) 24 cm
E) 25 cm.
- Sendo VP e VC os volumes das barras de chocolate de formato "paralelepípedo" e "cubo", respectivamente, e sendo a , a medida da aresta do cubo, temos:
VP = 3 cm . 18 cm . 4 cm = 216 cm3
VC = a3 VP = VC a3 = 216 cm3 ⇒ a = 6 cm
5)(Enem 2010) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.
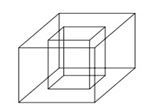
O volume de madeira utilizado na confecção desse objeto foi de:
A) 12 cm3
B) 64 cm3
C) 96 cm3
D) 1216 cm3
E) 1728 cm3
- O volume de madeira utilizado na confecção desse objeto será:
Volume do cubo externo – Volume do cubo interno = (12 cm)3 – (8 cm)3 = 1 216 cm3.
Alternativa D: 1.216 cm cúbicos
6)(Enem 2012) Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostrado na figura.
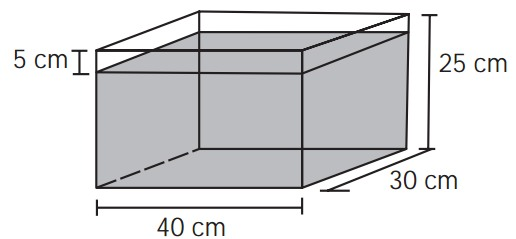
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2 400 cm3 ? Considere que o objeto ficou completamente submerso.
A) O nível subiria 0,2 cm, fazendo a água ficar com 20,2 cm de altura
B) O nível subiria 1 cm, fazendo a água ficar com 21 cm de altura.
C) O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura
D) O nível subiria 8 cm, fazendo a água transbordar
E) O nível subiria 20 cm, fazendo a água transbordar.
- O nível de água subirá 2 cm, pois, usando a fórmula de um prisma de base retangular, temos:
30 cm × 40 cm × x = 2 400 cm3 ⇔ x = 2 cm
Alternativa C: O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Volume do Cilindro
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Vamos estudar agora sobre o Volume de um cilindro... Há diversos materiais de formato cilíndrico presentes no nosso cotidiano, por exemplo: copos, latas de refrigerante, de ervilhas, pilhas etc.
Figura 7 e 8 - Exemplos de corpos cilíndricos

Fonte: Istock ()

Fonte: Istock ()
Volume do Cilindro
- Cilindro Reto
Cilindro reto é um sólido geométrico, portanto tem volume. Como no bloco retangular, podemos determinar o volume por meio do produto da área da base pela altura.
Figura 9 - Cilindro
Fonte: Acervo pessoal
Dessa forma o Volume do Cilindro reto é V cilindro= A base . h
Assim temos:
V = Ab.h
Vamos praticar!
Exemplo: Calcule o volume de um cilindro cuja altura mede 10 cm e o diâmetro da base mede 6,2 cm. Utilize o valor de 3,14 para π.
6,2 : 2 = 3,1. Logo, r: 3,1 cm; h: 10 cm
V = π.r2.h
V = π . (3,1)2 . 10
V = π . 9,61 . 10
V = π. 96,1
V = 3,14 . 96,1
V = 301,7 cm3
Exercícios de Fixação
8- O volume de uma lata cilíndrica é 942 centímetros cúbicos. Sabendo que a medida da altura dessa lata é 14 cm, determine a medida de seu raio. (Use π=3,14).
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios do Enem
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
7)(Enem 2010) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
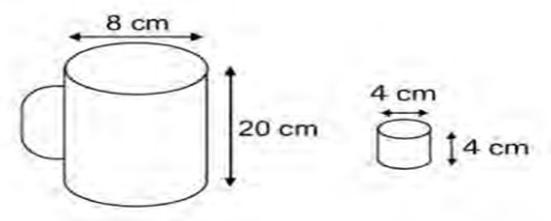
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá:
A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
- O volume do copinho plástico, em centímetros cúbicos, é π.2².4 = 16π
O volume da leiteira, em centímetros cúbicos, é π.4².20 = 320π
(Volume da leiteira) ÷ (volume do copinho) = 320π/16π = 20
Assim, para encher os vinte copinhos plásticos pela metade, é suficiente encher a leiteira até a metade.
8)(Enem) Uma artesã confecciona dois diferentes tipos de vela ornamental a partir de moldes feitos com cartões de papel retangulares de 20 m x 10 cm (conforme ilustram as figuras abaixo). Unindo dois lados opostos do cartão, de duas maneiras, a artesã forma cilindros e, em seguida, os preenche completamente com parafina.
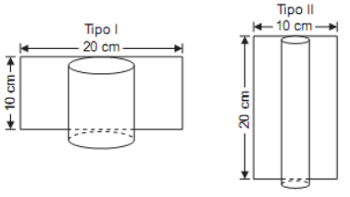
Supondo que o custo da vela seja diretamente proporcional ao volume da parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será:
a) o triplo.
b) o dobro.
c) igual.
d) a metade.
e) a terça parte.
- Para sabermos qual será a relação entre os custos teremos que calcular o volume da vela I e dividir pelo volume da vela II.
Para a vela I teremos que inicialmente descobrir seu raio. Sabendo que a vela é embalada pelo papel como na figura da esquerda, o comprimento da circunferência é dado por 2*π*r'. Como o comprimento da base é 20 cm, temos:
2*π*r' = 20
r' = 10/π cm
Portanto, o volume do cilindro será a área da base * altura. Como a área da circunferência é Ab = π*r², temos para o cilindro do tipo I:
V' = π*(r')²*h
Como r' = 10/π cm e h = 10 cm. Temos:
V' = π*(10/π)²*10
V' = π(100/π²)*10
Cancelando fatores comuns no numerador e denominador, temos que o volume da vela tipo I será:
V' = 1000/π cm³
Faremos agora o procedimento semelhante para a vela do tipo II. Primeiramente descobriremos o raio a partir do comprimento da circunferência. Que agora é de 10 cm. Logo:
2*π*r'' = 10
r'' = 5/π cm
Agora, sabendo o raio r'' = 5/π cm, a altura h = 20 cm podemos calcular o volume da vela de tipo II. Que será dado por:
V'' = Ab * h
V'' = π*r² * h
V'' = π*(5/π)² * 20
V'' = π*25/π² * 20
Cancelando o π, temos:
V'' = 500/π cm³
Como dito no início faremos a divisão entre o volume V' e V'' para sabermos o custo de uma em relação a outra:
Podemos cancelar π e dividir 1000/500 e assim temos que:
Portanto o custo da Vela tipo I em relação a vela tipo II é o dobro.
Alternativa B: o dobro
9)(Enem 2021) Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente,2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentara capacidade do tanque para que ele comporte900 peixes, mas sem alterar a sua profundidade. Considere 3 como aproximação para π.
O aumento da medida do raio do tanque, em metro, deve ser de:
a) √30 – 5
b) (√30 – 5)/2
c) √5
d) 5/2
e) 15/2
- Solução: questão muito interessante de geometria espacial do ENEM 2020 (Reaplicação/PPL) com uma aplicação prática da matemática. O volume do cilindro (Vc) é dado por:
Vc = π . R² . h
Inicialmente, o tanque está comportando 750 peixes, então podemos descobrir o seu volume usando uma regra de três simples:
5 peixes - 1 m³
750 peixes = x m³
5 . x = 750 . 1
x = 750/5
x = 150 m³
O volume inicial do tanque é de 150 m³, como a altura vale 2m, então podemos encontrar seu raio.
Vc = π . R² . h
150 = 3 . R² . 2
R² = 150/6
R² = 25
R = 5 m
Num segundo momento, o piscicultor decide aumentar o raio desse tanque e manter sua altura (2m), de modo que ele comporte 900 peixes, novamente podemos obter este volume usando uma regra de três simples.
5 peixes - 1 m³
900 peixes = x m³
5 . x = 900 . 1
x = 900/5
x = 180 m³
Hora de calcular o tamanho do raio do novo tanque.
Vc = π . R² . h
180 = 3 . R². 2
R² = 30
R = √30 m
Para encontrarmos o aumento que deve ser feito no raio do tanque, basta calcular (Raio Maior - Raio Menor). Sendo assim, o aumento da medida do raio do tanque, em metro, deve ser de ( √30 - 5 ) m.
Alternativa B: (√30 – 5)/2
10)(Enem 2021) Uma loja de materiais de construção vende dois tipos de caixas-d'água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d'água do tipo B é igual a 25% da altura da caixa-d'água do tipo A.
Se R denota o raio da caixa-d'água do tipo A, então o raio da caixa-d'água do tipo B é
a) R/2
b) 2 R
c) 4 R
d) 5 R
e) 16 R
- Solução: questão do ENEM 2020 sobre volume de cilindros. Essa é uma questão de geometria espacial que causa um pouco de dificuldades por não envolver números. Vamos resolvê-la passo a passo:
Seja o volume de um cilindro V = π . R² . h
Va = π . Ra² . ha
Vb = π . Rb² . hb
Sabemos que Va = Vb
π . Ra² . ha = π . Rb² . hb
Ra² . ha = Rb² . hb
Sabemos que hb = 0,25. ha e Ra = R
R² . ha = Rb² . 0,25. ha
R² = Rb² . 1/4
Rb² = 4R²
Rb = 2 R . [Alternativa correta é a letra B]
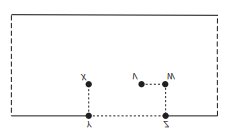
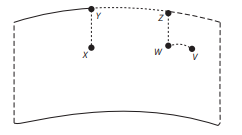
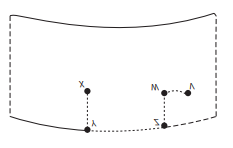
11)(Enem 2019) Uma formiga encontra-se no ponto X, no lado externo de um copo que tem a forma de um cilindro reto. No lado interno, no ponto V, existe um grão de açúcar preso na parede do copo. A formiga segue o caminho XYZWV (sempre sobre a superfície lateral do copo), de tal forma que os trechos ZW e WV são realizados na superfície interna do copo. O caminho XYZWV é mostrado na figura.
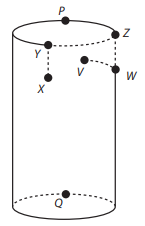
Sabe-se que: os pontos X, V, W se encontram à mesma distância da borda; o trajeto WV é o mais curto possível; os trajetos XY e ZW são perpendiculares à borda do copo; e os pontos X e V se encontram diametralmente opostos.
Supondo que o copo é de material recortável, realiza-se um corte pelo segmento unindo P a Q, perpendicular à borda do copo, e recorta-se também sua base, obtendo então uma figura plana. Desconsidere a espessura do copo.
Considerando apenas a planificação da superfície lateral do copo, a trajetória da formiga é:
A)
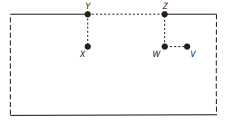
B)
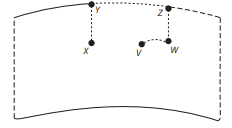
C)
D)
E)
12)(Enem 2019) Uma construtora pretende conectar um reservatório central (Rc) em formato de um cilindro, com raio interno igual a 2 m e altura interna igual a 3,30 m, a quatro reservatórios cilíndricos auxiliares (R1, R2, R3 e R4), os quais possuem raios internos e alturas internas medindo 1,5 m.
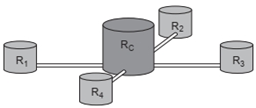
As ligações entre o reservatório central e os auxiliares são feitas por canos cilíndricos com 0,10 m de diâmetro interno e 20 m de comprimento, conectados próximos às bases de cada reservatório. Na conexão de cada um desses canos com o reservatório central há registros que liberam ou interrompem o fluxo de água.
No momento em que o reservatório central está cheio e os auxiliares estão vazios, abrem-se os quatro registros e, após algum tempo, as alturas das colunas de água nos reservatórios se igualam, assim que cessa o fluxo de água entre eles, pelo princípio dos vasos comunicantes.
A medida, em metro, das alturas das colunas de água nos reservatórios auxiliares, após cessar o fluxo de água entre eles, é
- 1,44.
- 1,16.
- 1,10.
- 1,00.
- 0,95.
13)(Enem 2018) Um artesão possui potes cilíndricos de tinta cujas medidas externas são 4 cm de diâmetro e 6 cm de altura. Ele pretende adquirir caixas organizadoras para armazenar seus potes de tinta, empilhados verticalmente com tampas voltadas para cima, de forma que as caixas possam ser fechadas.
No mercado, existem cinco opções de caixas organizadoras, com tampa, em formato de paralelepípedo reto retângulo, vendidas pelo mesmo preço, possuindo as seguintes dimensões internas:
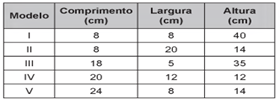
Qual desses modelos o artesão deve adquirir para conseguir armazenar o maior número de potes por caixa?
- I
- II
- III
- IV
- V
14)(Enem 2017) Um fabricante de creme de leite comercializa seu produto em embalagens cilíndricas de diâmetro da base medindo 4 cm e altura 13,5 cm. O rótulo de cada uma custa R$ 0,60. Esse fabricante comercializará o referido produto em embalagens ainda cilíndricas de mesma capacidade, mas com a medida do diâmetro da base igual à da altura.
Levando-se em consideração exclusivamente o gasto com o rótulo, o valor que o fabricante deverá pagar por esse rótulo é de:
a) R$ 0,20, pois haverá uma redução de 2/ 3 na superfície da embalagem coberta pelo rótulo.
b) R$ 0,40, pois haverá uma redução de 1/ 3 na superfície da embalagem coberta pelo rótulo.
c)R$ 0,60, pois não haverá alteração na capacidade da embalagem.
d) R$ 0,80, pois haverá um aumento de 1/ 3 na superfície da embalagem coberta pelo rótulo.
e) R$ 1,00, pois haverá um aumento de 2/ 3 na superfície da embalagem coberta pelo rótulo.
- As duas embalagens terão a mesma capacidade, ou seja, mesmo volume, e que o diâmetro da segunda embalagem vai ter o mesmo valor que sua altura. Portanto, o raio da segunda embalagem valera a metade da sua altura.
Primeiro, iguale os volumes das duas embalagens:
V1 = V2
π.R^2.H = π.r^2.h (corta o pi dos dois lados)
R^2.H = r^2.h
2^2 .13,5 = (h/2)^2 . h
54 = h^3 / 4
216 = h^3
h = 6
Em seguida, sabendo que o rotulo corresponde à área lateral da embalagem cilíndrica, você vai relacionar as áreas laterais das duas embalagens, pra saber o quanto aumenta ou diminui a segunda, em relação à primeira. Então:
A2/A1 = 2.π.r.h/2.π.R.H = r.h/R.H = 3.6/ 2.13,5 =18/27 = 2/3
Com o resultado anterior, conclui-se que houve uma redução de 1/3 da área lateral da embalagem, relação à primeira embalagem.
Valor do rotulo = 2/3 . 0,60 = 0,40
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Volume da Pirâmide
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
Agora é a vez da Pirâmide! Para calcular o volume de uma pirâmide, é importante saber que existem diferentes tipos de pirâmide, pois ela pode possuir a base formada por qualquer polígono, como um triângulo, um quadrado ou um hexágono. Dessa forma, o cálculo da área da base está ligado ao polígono correspondente.
Volume da Pirâmide
O volume da pirâmide corresponde a 1/3 de um prisma de mesma altura e base. Portanto, a expressão matemática utilizada no cálculo do volume da pirâmide é:
Figura 10 - Pirâmide do Egito

Fonte: Pixabay (https://cdn.pixabay.com/photo/2018 /06/16/10/10/pyramid-3478575__340.jpg)
V = (Ab * h) / 3
Ab = área da base h = altura
Vamos praticar! Exemplo I: Uma pirâmide de base quadrangular possui altura medindo 2 metros e cada lado da base com medida igual a 3 metros. Determine o volume dessa pirâmide.
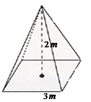
Exemplo II: Uma indústria irá fabricar uma peça no formato de uma pirâmide de base triangular com as medidas indicadas na figura. Sabendo que serão fabricadas 500 peças maciças de aço, determine o volume total de aço que será gasto na produção dessas peças.
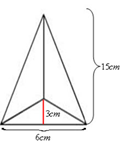
Exemplo III: A figura representa uma pirâmide de base pentagonal com lados regulares medindo 12 metros e a apótema da base medindo 8,2 metros, aproximadamente. Sabendo que a altura dessa pirâmide é igual a 20 metros, qual será sua capacidade sabendo que 1 m³ corresponde a 1000 litros?
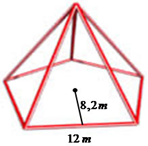
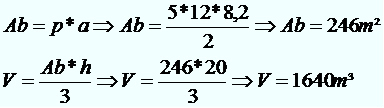
Se 1m³ corresponde a 1000 litros, temos que:
1640m³ = 1640 * 1000 = 1 640 000 litros de capacidade.
Exercícios de Fixação
9- Determine o volume da pirâmide regular de base triangular, de aresta da base com medida a=3 cm e altura h= raiz de 8 cm.
- Primeiro calcula a área da base Ab=(3*3)/2=4,5
agora achamos o volume:
dados:
Ab=4,5
h=√8
v=(Ab*h)/3
V=(4,5*√8)/3
V=1,5√8
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios do Enem
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
15)(Enem) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
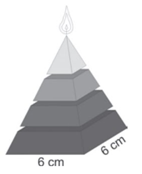
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
A) 156 cm³
B) 189 cm³
C) 192 cm³
D) 216 cm³
E) 540 cm³
- O volume de parafina gasto na nova vela corresponde à subtração do volume da pirâmide maior, com aresta da base de 6 cm e altura de 19 – 3 = 16 cm, pelo volume da pirâmide menor, com 1,5 cm de aresta da base e 4 cm de altura.
Como volume da pirâmide é calculado pela terça parte do produto da área da base pela altura, o volume de parafina, em cm³, é de 1/3.6.6.16 − 1/3.1,5.1,5.4 = 192 – 3 = 189 cm³.
Alternativa B: 189 centímetros cúbicos.
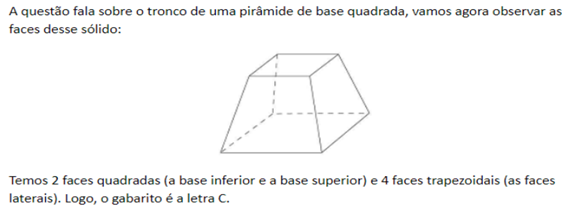
16)(Enem 2021) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são:
A) 2 quadrados e 4 retângulos.
B) 1 retângulo e 4 triângulos isósceles.
C) 2 quadrados e 4 trapézios isósceles.
D) 1 quadrado, 3 retângulos e 2 trapézios retângulos.
E) 2 retângulos, 2 quadrados e 2 trapézios retângulos.
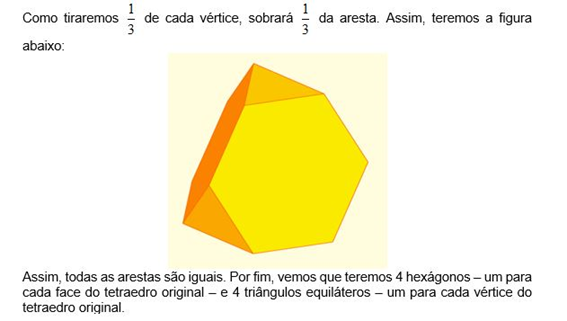
17)(Enem 2019) As luminárias para um laboratório de matemática serão fabricadas em forma de sólidos geométricos. Uma delas terá a forma de um tetraedro truncado. Esse sólido é gerado a partir de secções paralelas a cada uma das faces de um tetraedro regular. Para essa luminária, as secções serão feitas de maneira que, em cada corte, um terço das arestas seccionadas serão removidas. Uma dessas secções está indicada na figura.
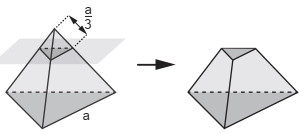
Essa luminária terá por faces:
A) 4 hexágonos regulares e 4 triângulos equiláteros.
B) 2 hexágonos regulares e 4 triângulos equiláteros.
C) 4 quadriláteros e 4 triângulos isósceles.
D) 3 quadriláteros e 4 triângulos isósceles.
E) 3 hexágonos regulares e 4 triângulos equiláteros.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Volume do Cone
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
A figura cone te faz lembrar do quê?
Figura 11 - O cone na Medicina Veterinária
Volume do Cone
Para calcular o volume do cone, é necessário calcular a área do círculo que forma a sua base. A fórmula é a mesma da circunferência: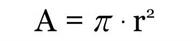
Depois precisa-se medir a altura do cone, já que ele é tridimensional. Para isso, multiplica-se a sua altura pela área da sua base:
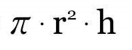
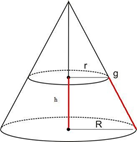
Agora divida a fórmula acima por três:
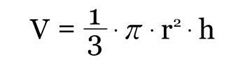
O cálculo do volume do cone é feito através da multiplicação da área da base pelo valor da sua altura. Dividindo o resultado por três.
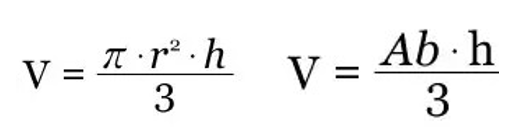
Vamos praticar!
Exemplo I: Tem-se um reservatório de água que possui a forma de um cone de revolução com 8 metros de profundidade. Sabe-se que o diâmetro da sua base mede 4 metros. Determine a capacidade, em litros, desse reservatório. (Use p = 3,14)
De acordo com o enunciado do problema: h = 8 m (profundidade)
r = d/2 = 4/2 = 2 m
Informar a capacidade é o mesmo que calcular o volume do reservatório. Portanto, a partir da utilização da fórmula do volume do cone, chega-se ao resultado:

Como o importante é saber a capacidade do reservatório em litros, deve-se lembrar da seguinte relação: 1 m³= 1000 litros.
Sendo assim, a capacidade do reservatório será:
V = 33,49 ×1000 = 33490 litros
Exemplo II: Uma piscina possui volume de aproximadamente 3000 m³ e diâmetro da base medindo 24 metros. Determine a altura desta piscina.
O valor do raio nesse exemplo é 12, porque o raio é metade do diâmetro, veja:
r = d/2
r = 24/2
r = 12
Agora que já se sabe o valor do raio, pode-se calcular o volume da piscina da seguinte maneira:
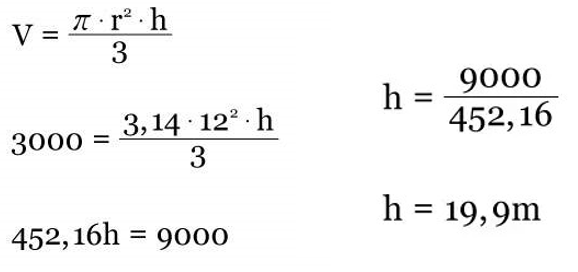
Logo, a altura da piscina é de aproximadamente 20 metros.
Exercícios de Fixação
10- (Cefet- SC) Dado um copo em forma de cilindro e outro de forma cônica de mesma base e altura. Se eu encher completamente o copo cônico com água e derramar toda essa água no copo cilíndrico, quantas vezes terei que fazê-lo para encher completamente esse copo?
a) Apenas uma vez.
b) Duas vezes.
c) Três vezes.
d) Uma vez e meia.
e) É impossível saber, pois não se sabe o volume de cada sólido.
O volume de um cilindro é dado pela expressão
A razão entre o volume do cilindro e do cone será
Como as medidas das alturas de ambos são iguais, podemos simplificar o termo h. Como as medidas das bases, que são círculos, são iguais, então, também possuem o mesmo raio r, que também será simplificado. Assim:
Logo, o volume desse cilindro é três vezes o volume desse cone e serão necessários 3 desses copos cônicos para encher um copo cilíndrico completamente. Alternativa C
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Volume do tronco de um Cone
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
- Volume do tronco de um Cone
Se cortamos o cone em duas partes, teremos a parte que contém o vértice e a parte que contém a base.
O tronco do cone é a parte mais larga do cone, ou seja, o sólido geométrico que contém a base da figura. Ele não inclui a parte que contém o vértice.
Assim, para calcular o volume do tronco do cone, utiliza-se a expressão:
V = π.h/3 . (R2 + R . r +r2)
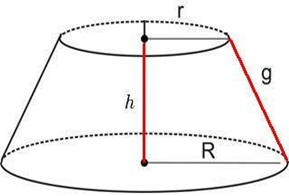
Onde:
V: volume do tronco do cone
π: constante que equivale a 3,14 aproximadamente
h: altura
R: raio da base maior
r: raio da base menor
Vamos praticar!
Exemplo I: Calcule o volume de um tronco de cone de 15 cm de altura sabendo que o raio da base menor mede 10 cm e o raio da base maior mede 20 cm.Temos todos os elementos necessários para calcular o volume do tronco de cone, uma vez que ele é dado em função da altura e da medida dos raios das duas bases. Assim, teremos:
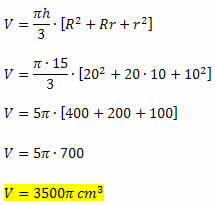
Exercícios de Fixação
11- Um depósito de grãos apresenta a forma de um tronco de cone cujo raio da base maior mede 12 metros e o raio da base menor tem 7 metros de comprimento. Calcule a capacidade desse depósito sabendo que sua altura é de 9 metros.- O volume de um cone circular reto é dado pela fórmula:
V = (π·r²·h) / 3
Como V = 4π, então:
4π = (π·r²·h) / 3
π·r²·h = 4π·3
π·r²·h = 12π
r²·h = 12π/π
r²·h = 12
"o raio da base é igual a dois terços da altura"
r = 2/3·h
r = 2h/3
Substituindo , temos:
r²·h = 12
(2h/3)²·h = 12
(4h²/9)·h = 12
4h³/9 = 12
4h³ = 12·9
4h³ = 108
h³ = 108/4
h³ = 27
h = ∛27
h = 3 m
Alternativa B
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios do Enem
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
18)(Enem 2018) A figura mostra uma anticlepsidra, que é um sólido geométrico obtido ao se retirar dois cones opostos pelos vértices de um cilindro equilátero, cujas bases coincidam com as bases desse cilindro. A anticlepsidra pode ser considerada, também, como o sólido resultante da rotação de uma figura plana em torno de um eixo.
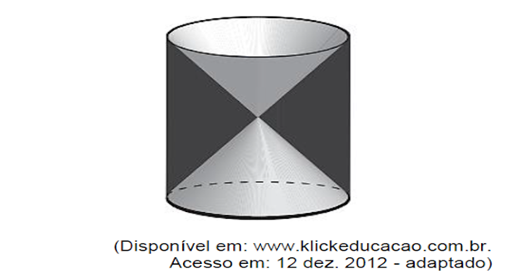
A figura plana cuja rotação em torno do eixo indicado gera uma anticlepsidra como a da figura acima é:
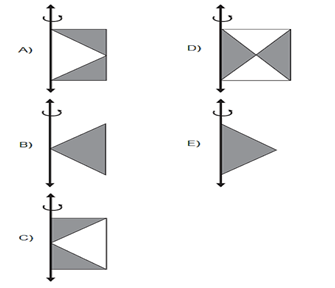
- O enunciado nos informa que, de um cilindro equilátero são retirados dois cones opostos pelo vértice. Da imagem abaixo, temos que os dois cones retirados estão destacados em cinza. Sendo assim, o sólido que restou é "vazado" em cima e embaixo, ou seja, nas bases do cilindro.
Vamos analisar cada figura das alternativas.
a) Não pode ser essa, pois ao rotacionarmos a figura, não teremos um vazamento nas bases.
b) A alternativa correta é essa.
Perceba que ao girarmos o triângulo, teremos os dois cones retirados inicialmente.
c) Não pode ser essa, pois teremos um vazamento na lateral.
d) Ao girarmos essa figura, não obteremos o sólido desejado.
e) Girando esse triângulo, teremos dois cones com as bases coincidentes.
Alternativa B
19)(Enem 2010) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura que deverá instalar a luminária ilustrada na figura.
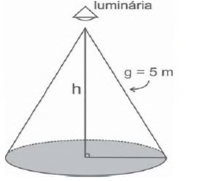
Sabendo-se que a luminária deverá iluminar uma área circular de 28,26 m2, considerando π ![]() 3,14, a altura h será igual a:
3,14, a altura h será igual a:
a) 3 m
b) 4 m.
c) 5 m.
d) 9 m.
e) 16 m.
Área da base=TT.r²
28,26=3,14.r²
r²=9
Aplicando Pitágoras
Hipotenusa²=Cateto²+Cateto²
g²=h²+r²
5²=h²+9
25=h²+9
h²=16
h=4
Alternativa B: 4 m
20)(Enem 2012) Nas empresas em geral, são utilizados dois tipos de copos plásticos descartáveis, ambos com a forma de troncos de cones circulares retos:
• copos pequenos, para a ingestão de café: raios das bases iguais a 2,4 cm e 1,8 cm e altura igual a 3,6 cm;
• copos grandes, para a ingestão de água: raios das bases iguais a 3,6 cm e 2,4 cm e altura igual a 8,0 cm.
Uma dessas empresas resolve substituir os dois modelos de copos descartáveis, fornecendo para cada um de seus funcionários canecas com a forma de um cilindro circular reto de altura igual a 6 cm e raio da base de comprimento igual a y centímetros. Tais canecas serão usadas tanto para beber café como para beber água.
Sabe-se que o volume de um tronco de cone circular reto, cujos raios das bases são respectivamente iguais a R e r e a altura é h, é dado pela expressão:
![]()
O raio y da base dessas canecas deve ser tal que y2 seja, no mínimo, igual a:
- 2,664 cm.
- 7,412 cm.
- 12,160 cm.
- 14,824 cm.
- 19,840 cm.
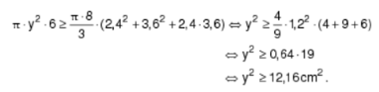
Alternativa C
21)(Enem 2011) Uma empresa responsável por produzir arranjos de parafina recebeu uma encomenda de arranjos em formato de cone reto. Porém, teve dificuldades em receber de seu fornecedor o molde a ser utilizado e negociou com a pessoa que fez a encomenda o uso de arranjos na forma de um prisma reto, com base quadrada de dimensões 5 cm x 5 cm.
Considerando que o arranjo na forma de cone utilizava um volume de 500 mL, qual deverá ser a altura, em cm, desse prisma para que a empresa gaste a mesma quantidade de parafina utilizada no cone?
- 8
- 14
- 20
- 60
- 200
- volume = área da base.altura
500 = Abase.altura
500 = (5.5 "calculando a área da base").altura
altura = 500/25(área da base 5.5)
altura = 20 cm
Alternativa C
22)(Enem 2014) Para fazer um pião, brinquedo muito apreciado pelas crianças, um artesão utilizará o torno mecânico para trabalhar num pedaço de madeira em formato de cilindro reto, cujas medidas do diâmetro e da altura estão ilustradas na Figura 1. A parte de cima desse pião será uma semiesfera, e a parte de baixo, um cone com altura 4 cm, conforme Figura 2. O vértice do cone deverá coincidir com o centro da base do cilindro.
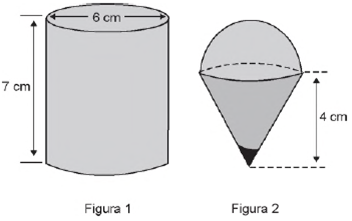
O artesão deseja fazer um pião com a maior altura que esse pedaço de madeira possa proporcionar e de modo a minimizar a quantidade de madeira a ser descartada.
Dados:
O volume de uma esfera de raio r é 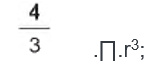 ;
;
O volume do cilindro de altura h e área da base S é S.h;
O volume do cone de altura h e área da base S é .S.h;
Por simplicidade, aproxime ∏ para 3.
A quantidade de madeira descartada, em centímetros cúbicos, é
a) 45.
b) 48.
c) 72.
d) 90.
e) 99.
- – Volume cilindro
Vci = pi.r².H = 3.3².7 = 189 cm³
– Volume semiesfera
Vs = [(4/3).pi.r³ ]/2= (2/3).3.3³ = 54 cm³
– Volume do cone
Vco = (1/3).pi.r².h = (1/3).3.3².4 = 36 cm³
Volume de madeira que será descartado
V = 189 – 54 – 36
V = 99 cm³
Alternativa E
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Razão
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
O último sólido a ser estudado é a esfera. Lembra dela nos campos de futebol!
Figura 12 - Estádio de Futebol

Fonte: Pixabay (https://cdn.pixabay.com/photo/ 2016/11/29/02/05/audience-1866738__340.jpg)
Volume de uma esfera
O volume da esfera é calculado através da seguinte fórmula:
Ve= 4. π. r3/ 3
Figura 13 - Bola de Futebol

Fonte: Pixabay (https://cdn.pixabay.com/photo/ 2013/07/13/10/51/football-157930__480.png)
Vamos praticar!
Exemplo I: Dada uma esfera qualquer com raio 5 cm, qual o seu volume?
Ve = 4.π.r2/3
Ve= (4. 3,14. 53) /3
Ve = (12,56. 125) /3
Ve = 1570/ 3
Ve = 523,33 cm3
Exercícios de Fixação
12- Dada duas esferas, A e B. O volume de A corresponde a 1/8 do volume de B, sabe-se também que o raio da esfera B mede 10 cm, qual o valor do raio e volume da esfera A?
- Solução: Calcular a capacidade do depósito é o mesmo que calcular seu volume. Temos que:
VeA = VeB/8 - 4.p.r³/3 = 4.p(10)³/3(8)
- 4.p.r³ = 4.p.(10)³/8
- r³ = 10³/2³
- r = 10/2
- r = 5
A esfera A possui raio de 5 cm. Agora vamos descobrir o seu volume:
- VeA = 4.p.r³/3
- VeA = 4. 3,14. 5³/3
- VeA = 4. 3,14. 125/3
- VeA = 1.570
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Exercícios do Enem
Como citar este documento: CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da; ALBUQUERQUE, Raquel Meneguini; ALCÂNTARA. Geometria Espacial – Volume. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/ cursinho/home/materias/geometria-espacial-volume.html. Acesso em: [data de acesso].
23)(Enem 2019) A gripe é uma infecção respiratória aguda de curta duração causada pelo vírus influenza. Ao entrar no nosso organismo pelo nariz, esse vírus multiplica-se, disseminando-se para a garganta e demais partes das vias respiratórias, incluindo os pulmões.
O vírus influenza é uma partícula esférica que tem um diâmetro interno de 0,00011 mm.
Disponível em: www.gripenet.pt. Acesso em: 2 nov. 2013 (adaptado).
Em notação científica, o diâmetro interno do vírus influenza, em mm, é:
- 1,1 × 10-1
- 1,1 × 10-2
- 1,1 × 10-3
- 1,1 × 10-4
- 1,1 × 10-5
24)(Enem 2015) Na imagem, a personagem Mafalda mede a circunferência do globo que representa o planeta Terra.

Em uma aula de matemática, o professor considera que a medida encontrada por Mafalda, referente à maior circunferência do globo, foi de 80 cm. Além disso, informa que a medida real da maior circunferência da Terra, a linha do Equador, é de aproximadamente 40 000 km.
QUINO. Toda Mafalda. São Paulo: Martins Fontes, 2008 (adaptado).
A circunferência da linha do Equador é quantas vezes maior do que a medida encontrada por Mafalda?
- 500
- 5 000
- 500 000
- 5 000 000
- 50 000 000
- Temos que 40.000 km = 4.000.000.000 cm
Assim, esse valor dividido por 80 resulta em 50.000.000
Temos que 40.000 km = 4.000.000.000 cm
Assim, esse valor dividido por 80 resulta em 50.000.000
25)(Enem 2016) A bocha é um esporte jogado em canchas, que são terrenos planos e nivelados, limitados por tablados perimétricos de madeira. O objetivo desse esporte é lançar bochas, que são bolas feitas de um material sintético, de maneira a situá-las o mais perto possível do bolim, que é uma bola menor feita, preferencialmente, de aço, previamente lançada. A Figura 1 ilustra uma bocha e um bolim que foram jogados em uma cancha. Suponha que um jogador tenha lançado uma bocha, de raio 5 cm, que tenha ficado encostada no bolim, de raio 2 cm, conforme ilustra a Figura 2.
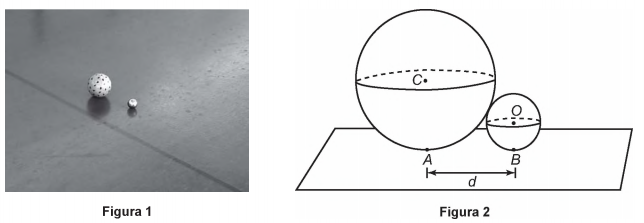
Considere o ponto C como o centro da bocha, e o ponto O como o centro do bolim. Sabe-se que A e B são os pontos em que a bocha e o bolim, respectivamente, tocam o chão da cancha, e que a distância entre A e B é igual a d. Nessas condições, qual a razão entre d e o raio do bolim?
- 1
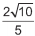
- √10/2
- 2
- √10
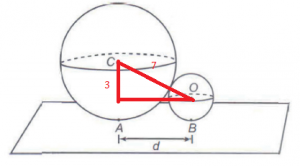
Utilizando o teorema de Pitágoras
Logo a razão entre o valor da distância d e o raio do bolim é:
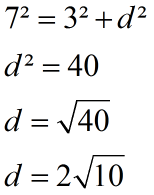
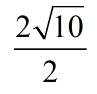
, simplificando temos :
![]()
26)(Enem 2016)Uma indústria de perfumes embala seus produtos, atualmente, em frascos esféricos de raio R, com volume dado por 4/3 π .(R)3.
Observou-se que haverá redução de custos se forem utilizados frascos cilíndricos com raio da base R/3 , cujo volume será dado por π (R/3)2 . h, sendo h a altura da nova embalagem.
Para que seja mantida a mesma capacidade do frasco esférico, a altura do frasco cilíndrico (em termos de R) deverá ser igual a:
- 2R.
- 4R.
- 6R.
- 9R.
- 12R.
- Para que tenhamos a mesma quantidade, deveremos ter :
Vesf=Vcili -> π.R³ = π.(R/3)²
R³=h.R²/9 -> h=12r
Alternativa E
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021