Exemplo 1

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Por exemplo, imagine que a professora do seu curso decidiu fazer uma gincana solidária de arrecadação, onde 15 alunos estão divididos em 3 grupos de 5 alunos cada, e a equipe vencedora ganhará um piquenique para passar a tarde no parque da cidade. A organização dos grupos está representada a seguir:

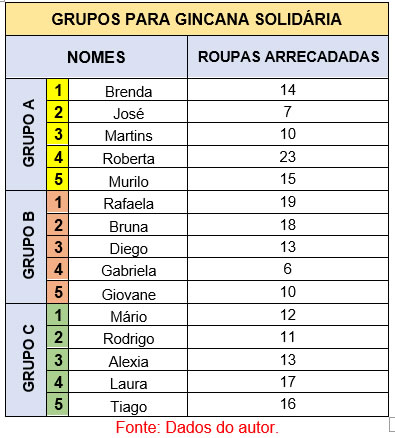
Vence a gincana a equipe que:

1. Tiver a maior média de roupas arrecadadas pelo total de alunos no grupo.
2. Em caso de empate na média, o critério de desempate será quem tiver menor desvio padrão.

A premiação será individual para cada aluno que:

1. Fizer parte da moda do agrupamento da sala.
2. Representar a mediana do total de doações por aluno na sala.

Você deve estar se perguntando em como descobrir quem será a equipe vencedora, por isso vem com a gente que descobriremos a seguir.

Infinidade de utilizações
            Você pode utilizar a estatística e as tabelas em tudo na sua vida, alguns exemplos estão a seguir.

Fonte: Pixabay: Disponível em: https://pixabay.com/pt/photos/estoque-negocia%C3%A7%C3%A3o-monitor-neg%C3%B3cios-1863880/

 

1. Bolsa de valores e mercado financeiro.
2. Recurso de aprimorar ideias ou aumentar as probabilidades de sucesso em determinada análise.
3. Instrumentação e medição de objetos.
4. Controle de qualidade preciso em qualquer empresa.
5. Aumento das chances de ganhar em na mega-sena!
6. Controle estatístico de processo.
7. Pesquisas populacionais ou amostrais, censos, pesquisas de campo etc.

Espera-se que ao fim deste capítulo você tenha desenvolvido as seguintes habilidades:

1. Analisar tabelas e gráficos de diversas formas, entender a etapa de construção delas e interpretá-las para a necessidade apresentada;
2. Transformar quaisquer números ou informações de maneira precisa e estruturada;
3. Calcular parâmetros estatísticos básicos;
4. Desenvolver o aprendizado em situações problema vivenciadas no cotidiano.

Um pouco mais!
O vídeo a seguir apresenta uma visão geral dos benefícios advindos da adoção da estatística na vida de cada um, assim como as aplicações nas diversas áreas do conhecimento.

Onde tudo começa...

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Onde tudo começa...
O estudo aqui realizado traz uma síntese prática e direcionada para aplicação básica da estatística em situações do dia a dia, bem como vai de encontro ao que é cobrado no Exame Nacional do Ensino Médio (ENEM).
Mas para desenvolver todas as habilidades contempladas neste capítulo, é necessário compreender alguns conceitos iniciais:

• Dados: são todas as informações presentes em uma determinada observação, elas podem ser de caráter:
• Quantitativos: descrevem quantidades ou valores de algo.

Exemplo: dezessete, seis pessoas, primeiro, oitavo, quinze metros, velocidade etc.

• Qualitativos: descrevem nomes ou características não passíveis de serem quantificadas para determinada situação a ser observada.

Exemplo: nome de pessoas, país, lugar, cores, adjetivos, entre outros.

• Tabelas: conjunto ou agrupamento de dados organizados visualmente em linhas e colunas com o objetivo de observar um fenômeno ou relação entre dados. Por exemplo:

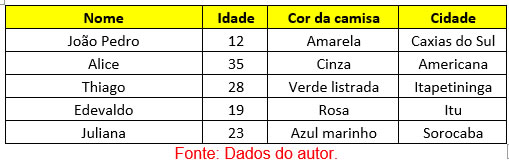
Fonte: Dados do autor.

• Atributo: podendo ser um ou vários, são as características ou propriedades quantitativas/qualitativas a serem analisadas de um determinado dado expresso numa linha ou coluna da tabela.

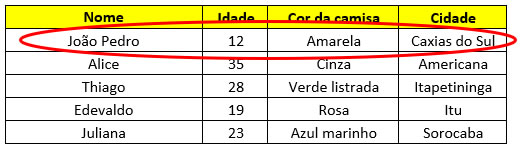
Fonte: Dados do autor.

• Frequência: refere-se a quantas vezes um determinado elemento se repete na situação analisada. São representadas na tabela após uma contagem simples, por um número. Observe:

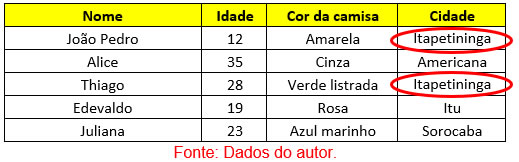
Fonte: Dados do autor.
Note que a cidade Itapetininga (dado qualitativo) se repete em dois momentos, isso descreve uma frequência de repetição igual a 2. Esse padrão se estende para todos os tipos de tabela, onde ela expressa a quantidade de aparições ou repetições para um dado.

• Gráficos: eles consistem em formas de representar as informações presentes em uma tabela, a fim de facilitar a compreensão da análise feita.

• Barras (ou colunas): as barras são orientadas no sentido vertical ou horizontal. Sua regra de formação consiste em:
• Cada nome ou informação deve ser colocada em uma única coluna.
• O tamanho dessa coluna depende do atributo para esse dado.
• Linhas: demonstram os valores em uma escala, facilitando assim a leitura das informações.

Com base na gincana, verificou-se somente para o grupo A, a quantidade de doações de cada integrante em um gráfico de barras.

.

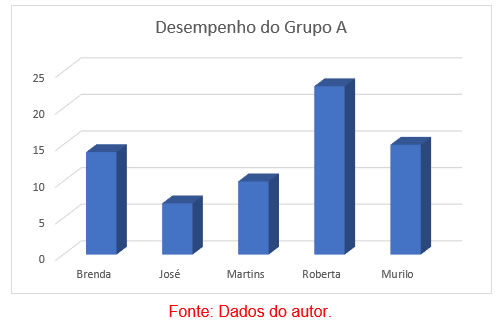
Note que cada aluno possui uma coluna e sua quantidade de arrecadação está disposta na vertical, demonstrando visualmente a proporção entre os alunos do mesmo grupo.
Transpondo-se corretamente a tabela para o gráfico, os benefícios serão altos. Observe o seguinte comparativo:

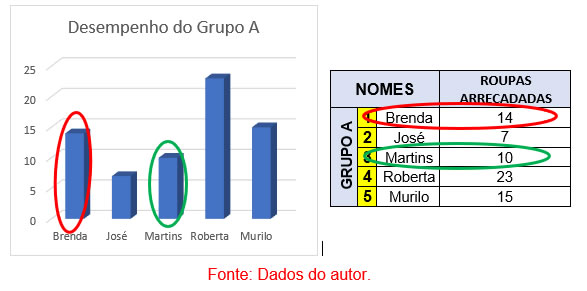
A correta transposição foi demonstrada, o procedimento é o mesmo para os outros tipos de gráfico, a diferença se dá pela adoção da melhor ferramenta para representar as informações.

• Setor circular: sendo outra forma de representar um desempenho ou quantidade, o gráfico de setor circular ou pizza apresenta:
• Área (tamanho) do setor circular para demonstrar a proporção de quantidade.
• Cada dado da tabela possui um setor e uma cor diferente, o tamanho define a quantidade de cada um.
• A legenda para identificação de qual dado está sendo abordado é primordial.
• As áreas dos setores circulares precisam ser exatamente proporcionais com o real encontrado na tabela.

Para o grupo B da gincana, observe a proporção de roupas arrecadadas e a quantidade em cima de cada setor circular.

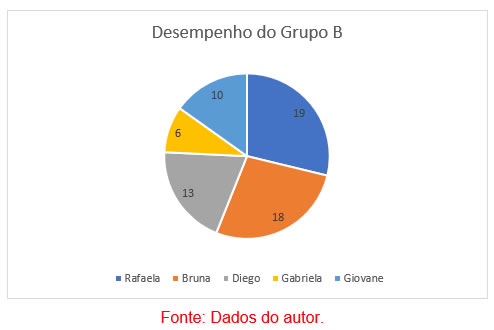
Observe a relação entre o gráfico de pizzas com a tabela de doações para o grupo B.

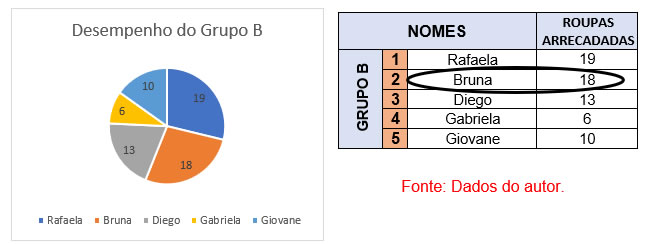
A aplicação desse tipo de gráfico é relativamente alta em pesquisas e censos que envolvem grande quantidade de dados.

• Linha: essa espécie de gráfico também é muito usual, e seu principal objetivo é:
• Descrever uma sequência de dados ao longo de um tempo contínuo.
• Essa sequência de dados deve ser a mesma para se observar uma evolução desse objeto de estudo.

Nesse sentido, os principais elementos do gráfico são:

• Eixo vertical: exibe a propriedade quantitativa a ser analisada.
• Eixo horizontal: demonstra o tempo que se passa.
• Pontos: é a relação entre o valor no eixo vertical e horizontal. A união entre os pontos é feita pela linha.
• Linha: demonstra visualmente toda a relação dos dados nos eixos, interligando os pontos.

Gráficos

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Suponha que a mesma gincana solidária de arrecadação se efetuou durante um ano, sendo 12 meses os elementos para se analisar. Observe um exemplo de gráfico de linha a seguir, identificando os elementos desse tipo.

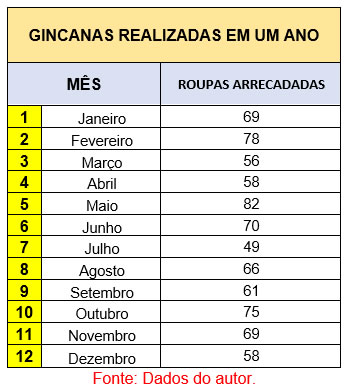
Com os dados dessa tabela, o gráfico de linhas é gerado, demonstrando todas as informações aqui apresentadas. Observe:

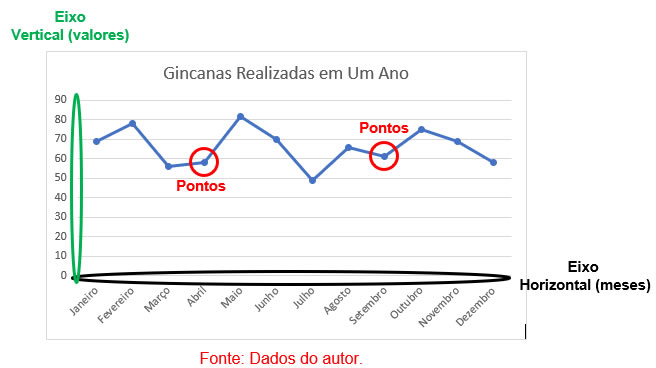
Além desses gráficos existem tantos outros, como:

1. Dispersão
2. Cone
3. Porcentagens
4. Áreas
5. Pirâmide
6. Histogramas
7. Distribuição normal

combinação entre elas pode gerar resultados muito positivos, representando dados de grande importância para sua aplicação. A imagem anterior representou esses tipos de gráfico em diversos aspectos, entender a sua diversidade e saber interpretar as estruturas em comum é de extrema importância.

Fonte: QuestionPro  Disponível em:  https://www.questionpro.com/blog/pt-br/amostragem-sistematica-simples-e-facil

Fonte:Pixabay. Disponível em: https://pixabay.com/pt/illustrations/gr%C3%A1fico-gr%C3%A1fico-de-pizza-neg%C3%B3cios-963016/

1. Estatística descritiva: leva em consideração os dados já coletados, eles podem ser estruturados nessa etapa, obtendo os cálculos estatísticos que servirão de base para 90% da maioria das aplicações. Como o próprio nome diz, ela descreve algo por meio de cálculos e conceitos.

Fonte: Pixabay. Disponível em: https://pixabay.com/pt/photos/roleta-mesa-de-roleta-fichas-5012427/

1. Estatística indutiva: nessa etapa o estudo torna-se mais aprofundado, pois com a parte descritiva apresentada, é possível realizar diversos estudos embasados na indução de valores, testes, probabilidades etc.

Aqui será adotada somente a estatística descritiva.

Instrumentos para análise estatística
Medidas de tendência central

A estatística descritiva tem forte relação com as medidas de centralidade, que basicamente expressam o agrupamento de resultados obtidos na zona central de um determinado conjunto de dados, ou seja, retornam e comparam os valores que estão na zona intermediária dessa amostra ou população. Entre os principais instrumentos utilizados para analisar

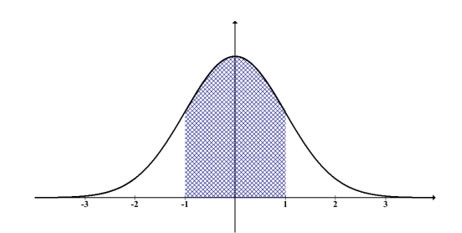
Fonte:Pixabay: Disponíve em:  https://pixabay.com/pt/vectors/distribui%C3%A7%C3%A3o-normal-estat%C3%ADsticas-159626/

os dados por meio de uma tendência dos dados do centro são a média, moda, mediana e desvio padrão.

Média aritmética
A média expressa o valor central para um conjunto de dados, ela relaciona todo o conteúdo da amostra em relação ao número delas. Com a média é possível demonstrar um valor de referência para determinado conjunto de dados. Por exemplo, ao estabelecer a média das alturas dos alunos em uma sala de aula pode-se comparar com o resultado de outras turmas e verificar se, no geral, uma sala tem alunos mais altos que em outras.
Vejamos o caso a seguir!
Para uma loja fictícia, o total de vendas no mês foi contabilizado para os 4 funcionários da equipe, eles são: Jorge, Camila, Aurora e Bruno. A montagem dá tabela se dá em:

1. 2 colunas: uma para os nomes dos funcionários, outra para o valor em reais de vendas.
2. 4 linhas: pois se trata de quatro funcionários nessa loja.

Observe a formação na tabela a seguir:

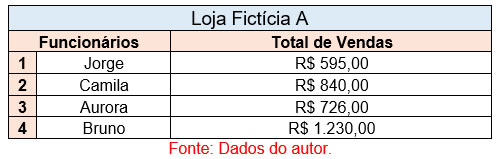
Cada um dos funcionários vendeu uma quantidade específica, porém o mais importante para a loja é saber quanto foi o valor ganho por pessoa. Observe a obtenção da média geral de lucro para determinada loja.
Para encontrar a média e o total de vendas para essa empresa, faz-se utilizar as seguintes expressões:
A média aritmética sempre leva em consideração a somatória dos valores em uma tabela, dividindo-se pela incidência desses dados, ou seja, a própria frequência (número de repetições n), como a seguir:

Diante do que vimos é possível generalizar o cálculo da média aritmética por meio da expressão:

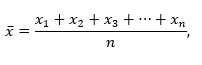
onde:
: média aritmética simples, a barra superior indica o valor de média, podendo ser expresso por m ou qualquer outra letra.
: somatória de cada valor para o conjunto de n elementos.
: número total de dados que estão sendo analisados, a somatória vai do primeiro elemento i até o último n.

Para a tabela da loja fictícia em questão:

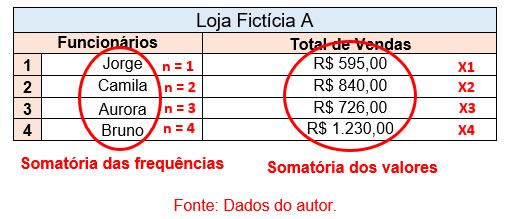
Após os cálculos realizados, conclui-se que a média de vendas nessa loja é de R$847,75.

 

Média ponderada

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Também muito utilizada na estatística, a média ponderada leva em consideração outro ponto relevante já citado aqui: a frequência!
Como demonstrado, a frequência diz respeito ao número de repetições para um mesmo dado fornecido, se um dado constituinte da tabela é encontrado uma única vez, sua frequência representa 1.
Além da frequência, a média ponderada utiliza o conceito peso para realização dos cálculos. Dizer que algo possui peso maior que o outro é considerar esse dado valendo tantas vezes mais, remetendo ao mesmo conceito de frequência.
Então, se o peso é levado em consideração, temos que:

Levando em consideração a média ponderada para um assunto cotidiano onde:

Fonte:  Pixabay: Disponível em: https://pixabay.com/pt/photos/escala-equil%C3%ADbrio-mundo-globo-2634833/

O que vale mais: A natureza ou o dinheiro?
Quando se trata de assunto, sempre nos perguntamos o que pesa mais na balança. Com a média não é diferente, avaliamos situações em que algumas coisas valem mais que as outras.

Se pudéssemos quantificar as informações da imagem anterior:

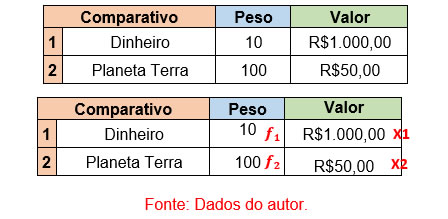
Para a tabela, observa-se que um elemento pesa mais que o outro, por isso deve-se multiplicar o valor pelo seu peso. Adequando-se a expressão apresentada temos:

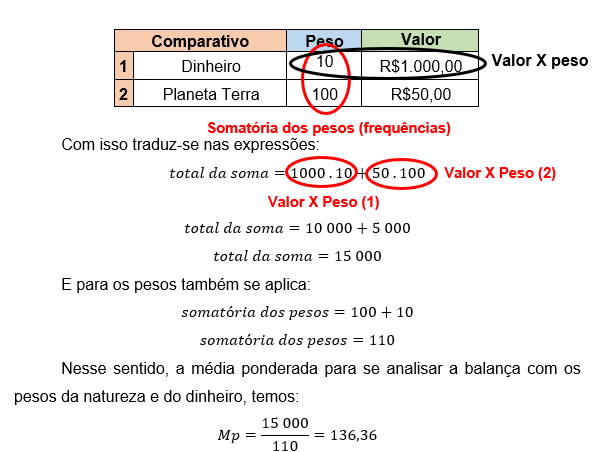
Então a média ponderada é de aproximadamente R$136,36 para essa balança da natureza ou do lucro.

Considerando os conceitos e os termos trabalhados anteriormente, temos que a média ponderada representa por:

 

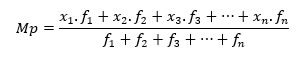
Exemplo 1:
Para uma loja fictícia alguns produtos foram vendidos no mês, e para uma futura reposição, todas as informações de quantidade, preço e tipo foram especificadas em uma tabela que é visualizada a seguir:

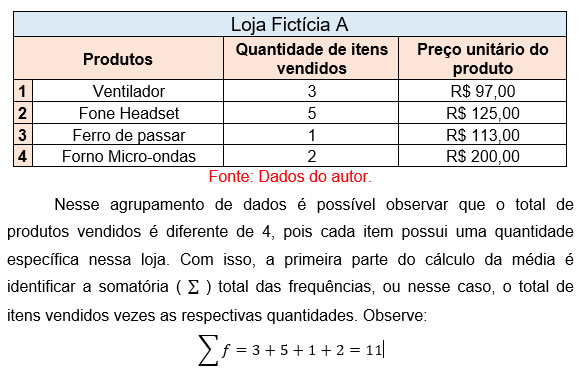
O total de itens para se calcular a média corresponde a 11. Com isso agora resta o cálculo do preço unitário de cada item multiplicado pela sua quantidade de venda.

Com a somatória dos valores (dividendo) e a somatória das frequências (divisor), obtém-se a média ponderada dos preços em relação à quantidade de produtos vendidos na loja:

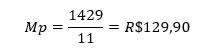
Conclui-se que a média de preço por produto está em R$129,90.

Exemplo 2:
Para maior entendimento, o segundo exemplo apresenta uma tabela contendo as notas de um estudante no curso de estatística no Instituto Federal de São Paulo em Itapetininga. Nesta disciplina o professor avalia as notas com pesos diferentes, pois para ele um seminário muito bem apresentado é mais importante que uma prova objetiva em sala de aula. Com isso a tabela a seguir apresenta as avaliações e seus respectivos pesos.

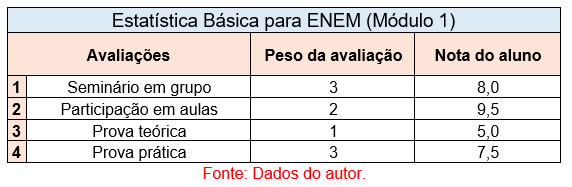
Para a tabela de notas em questão, observa-se a diferença entre os pesos, com isso o cálculo se inicia utilizando a mesma metodologia apresentada no exemplo anterior:

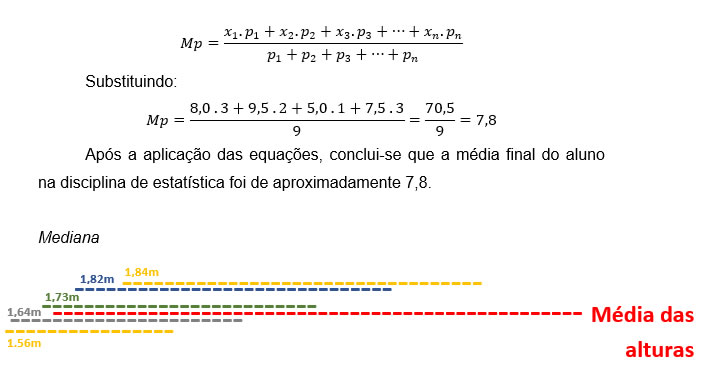
Para fins práticos, será adotada a segunda expressão final para cálculo da média ponderada:

Fonte: Dreamstime. Disponível  em  https://pt.dreamstime.com/ilustra%C3%A7%C3%A3o-stock-medida-da-altura-e-da-idade-do-crescimento-da-menina-%C3%A0-mulher-vetor-image88615401

A mediana também fazendo parte do conjunto de centralidade, desempenha um papel bastante interessante na estatística, pois além da média em um determinado conjunto, o valor que ocupa a posição central dele muitas vezes é diferente. Com isso a mediana quer representar o elemento do meio em um conjunto com n elementos ordenados de modo crescente (do menor para o maior) ou decrescente (do maior para o menor).
Muitas vezes a mediana é diferente da média, como que, em alguns casos, eles podem expressar o mesmo valor.
Para o primeiro exemplo observe que se a mediana ocupa a posição central, intuitivamente notamos que a representará a altura de 1.73m. Mas será que sempre a solução será visual assim?
Agora veremos a maneira sistemática de obter a mediana em qualquer conjunto de dados. Trata-se de uma sequência de procedimentos para serem realizados. O primeiro conceito consiste em identificar se o conjunto é:
PAR ou ÍMPAR
Com base nessa decisão temos:

• Elemento central no conjunto de n dados em valor ÍMPAR:

           

Para elementos ímpares, sempre existirá um elemento exatamente no centro desse conjunto de dados. Observe o conjunto a seguir que contém 5 elementos:

Para a imagem inicial verificamos:

1. A quantidade de 5 elementos.
2. Foi visto que a mediana representa o terceiro elemento.
3. Tabelamos a altura das 5 mulheres na imagem, importando ressaltar a sequência em ordem crescente:

 

 

Mediana para o conjunto de n dados em valor PAR:

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Fonte: Pixabay. Disponível em: https://pixabay.com/pt/illustrations/pessoas-formas-tamanhos-pessoa-3273195/

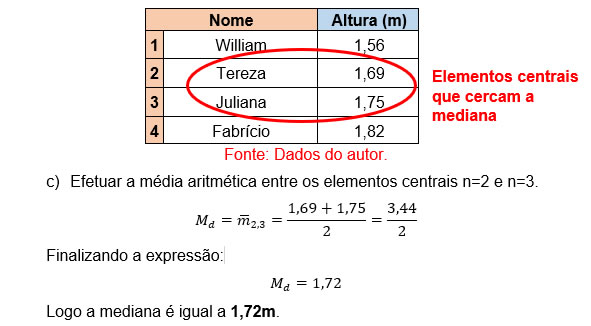
Note que na imagem anterior, a média das alturas expressam um valor, porém as duas pessoas que ocupam a posição de mediana (central) são de altura diferente. Para uma análise mais concisa, vamos tabular as informações contidas no exemplo, colocando nas colunas a lista de nomes e as respectivas alturas e nas linhas cada nome com a referida altura, obtendo:

A altura média para esse agrupamento de quatro pessoas é de 1,71 metro.
Mas para esse sistema, somente a altura da pessoa que fica na posição central é relevante. Por esse motivo, a obtenção da mediana se baseia na realização de uma sequência de etapas, estas que são:

1 - Calcular o total de elementos que estão sendo analisados, ou seja, encontrar o valor para n.

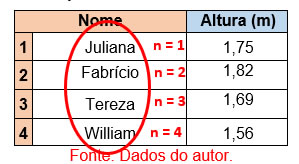
2 - Classificá-los em ordem crescente, ou seja, estruturar os n elementos do menor para o maior.

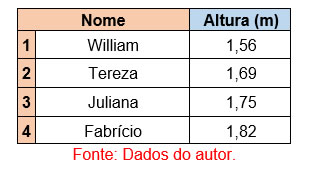
Esse passo é fundamental para o sucesso na obtenção de quaisquer valores para mediana.

A fim de resolver o problema anterior, adotaremos o cálculo da média aritmética entre os valores que cercam o elemento mediano obtido anteriormente. Observe:

Exemplo 1:
A tabela a seguir demonstra a idade de diversas pessoas:

Com isso, conclui-se que a mediana ocupa o elemento 5, que representa a idade 17. Logo a mediana para esse conjunto de 9 pessoas é igual a 17 anos, como na imagem a seguir:

Nesse sentido, a mediana seria o elemento 6,5. Porém já é visto que não existe nesse conjunto, por isso deve-se selecionar os dois elementos que cercam o elemento da mediana obtido, observe:

O elemento calculado 6,5 está entre os elementos 6 e 7, para encontrar a mediana basta realizar a média aritmética entre o valor que ocupam esses dois elementos:

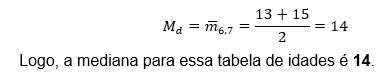
Com esse conhecimento em medidas de tendência central, o próximo passo será dado, e ele é relacionado à moda.

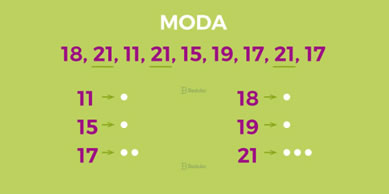
Com bastante uso na estatística, o conceito de moda entra em tendência central representando a repetição de elementos dentro de um conjunto de dados, ou seja, a moda expressa os dados que possuem maior frequência no mesmo conjunto.
Observe que na imagem anterior, o elemento 21 se repete 3 vezes, e ele é o único que possui maior repetição, ou seja, maior frequência. Com isso a moda para essa imagem é 21!

Seu conceito é simples, porém requer atenção para a sua análise. Para demonstração, algumas das tabelas já estudadas entrarão em uso para obtenção da moda. Observe a seguir o conjunto de alunos em uma sala de aula no curso de estatística:

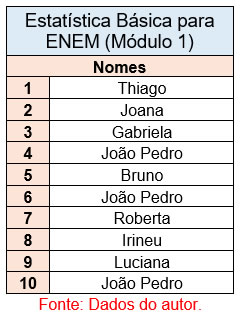
Analisando esse agrupamento de nomes, conclui-se que o nome João Pedro aparece 3 vezes na tabela, mesmo sendo 3 pessoas diferentes e provavelmente com sobrenomes diferentes também, o estudo aqui está referindo-se ao nome, com isso é possível converter a tabela em uma nova reagrupada em frequência:

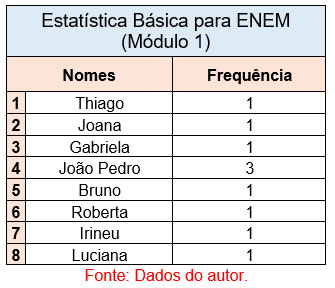
Após a montagem da nova tabela, fica nítido o conjunto de nomes que possui maior frequência ou maior repetição, logo a moda para o curso de estatística básica é o nome João Pedro.
Além disso, existem mais algumas denominações para a moda em um conjunto de dados, elas são:

a) Conjunto sem moda ou amodal: quando os dados não possuem repetição ou frequência diferente de 1. Exemplo:

Esse conjunto é denominado amodal, pois atende ao requisito demonstrado. Note que a moda não interfere o cálculo de média ou mediana, porém todos constituem o conjunto de medida central.

b) Conjunto com duas modas ou bimodal: como o próprio nome diz, dois dados estão se repetindo em igual frequência. Vale destacar que, em um conjunto apresentando frequências diferentes de 1, mas que possuem diferença entre as repetições dos outros dados, não caracteriza um conjunto bimodal. Observe:

Aqui temos destacados duas repetições, uma delas é em 15 anos (frequência 2) e a outra é em 11 anos (frequência 2). Nesse contexto temos um conjunto bimodal, pois temos dois dados repetindo mais e a frequência em que repetem é igual.
Observe esse segundo caso:

Nessa situação também temos dois dados repetindo, porém a frequência de 15 anos é maior que para 11 anos (3 e 2, respectivamente), com isso o conjunto possui apenas uma moda, que corresponde a 15 anos.

c) Conjunto com três modas ou trimodal: obedecendo aos critérios apresentados anteriormente, o conjunto trimodal representa 3 dados repetindo com frequências iguais umas às outras. Observe o exemplo a seguir:

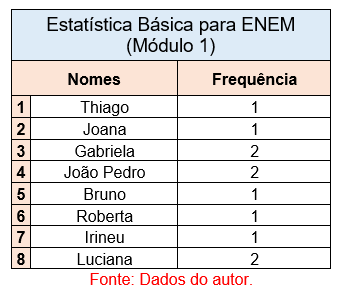
Nessa sala se observa 3 nomes repetindo mais de uma vez, e eles apresentam frequências iguais a 2, temos aqui um exemplo de um conjunto trimodal.
Estar atento a esses detalhes garante sucesso na interpretação de tabelas e a realização dos cálculos de média e mediana complementam o conjunto de medidas de tendência central, implicando em uma excelente base para o vestibular, assim como para a sequência do conteúdo em estatística.
O próximo tópico estudado entrará na base para o estudo de dispersão de dados em estatística, também possui enorme importância em qualquer empresa ou aplicação. Seu entendimento se estende aos limites de vestibulares, porém é requisito mínimo em todas as áreas de conhecimento que desejar se aplicar.

Um pouco mais!

O vídeo a seguir sintetiza o conteúdo estudado até aqui, ele é apresentado de uma maneira interativa e conclusiva sobre os termos e conceitos descobertos:

 

Desvio padrão e variância

Como citar este documento: NASCIMENTO, Felipe Delgado do; CAMPOS, Ayumi Kato de; CRUZ, Paulo Henrique Correia Araújo da. Estatística. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/estatistica.html. Acesso em: [data de acesso].

Partindo das medidas de tendência central, surgem os conceitos de variância e desvio, eles oferecem suporte à média, além de representarem o grau de confiabilidade e exatidão no conjunto de dados.
Como o próprio nome já diz, essa descrição de dados estima um valor padrão para a variação dos valores que são obtidos em determinada amostra e:

• Quanto maior for o desvio: maior a dispersão dos dados arranjados, ou seja, eles variam muito ao longo do sistema, com isso fica difícil de se estabelecer um padrão para as próximas amostras, assim como a confiabilidade diminui.
• Quanto menor for o desvio: menor a dispersão dos dados, a variação dos mesmos dados é menor, desempenhando assim maior precisão para uma futura avaliação dos dados, além do aumento de confiabilidade no sistema.

A interpretação do desvio vem em conjunto com a média, sempre que ela for encontrada, o mais interessante a destacar é o desvio padrão desse conjunto, pois este, como será visto posteriormente, é uma taxa de variação média que se aplica em todos os dados. Graficamente o desvio está numa faixa de valores em que o próximo dado a ser encontrado pode estar, isso também tem relação com probabilidade. Observe:

Entender a aplicabilidade e a correta adequação da expressão matemática são pontos chave desse assunto, por isso utiliza-se o modelo de vendas para uma loja fictícia, onde deseja-se obter o desvio padrão das vendas em reais, para um conjunto de 4 funcionários analisados nessa mesma loja. Observe a seguir:

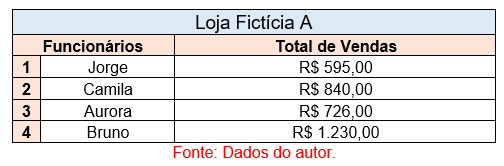
Utilizando a mesma situação descrita no outro tópico, tem-se que a média é igual a R$847,75. Porém muitos valores estiveram longe desse resultado, por esse motivo calculamos a diferença entre cada elemento e a respectiva média do sistema:

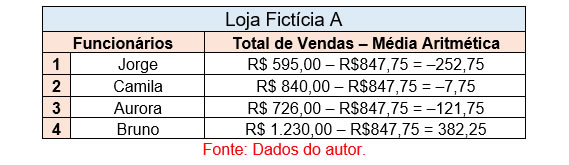
Nesse sentido, a variação entre elas poderá ser expressa negativamente, porém a diferença sempre deve ser considerada em valores absolutos! Para isso, eleva-se essa diferença ao quadrado. Observe:

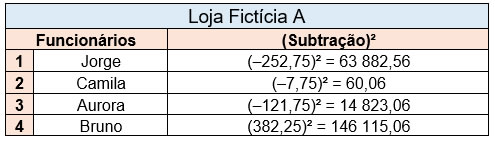
Fonte: Dados do autor.

Como o sistema se trata de um valor que é médio para todo o conjunto, a próxima etapa consiste em efetuar a razão entre a somatória dos quadrados das diferenças em valor absoluto e a sua frequência ou quantidade de elementos, obtendo o que chamamos de variância. Observe:

Após esse procedimento, conclui-se que o desvio padrão para esse exemplo é de aproximadamente R$237,11, isto é, o total de vendas pode ser R$ 237,11 maior ou menor que a média por vendedor. O seu esquema de variação é demonstrado a seguir.

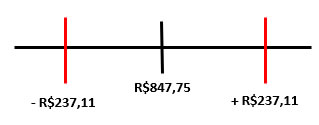
Exemplo:
Em uma indústria foi necessário medir algumas peças que estavam bloqueadas por apresentarem defeito na análise de qualidade, foram coletadas amostras de cada lote desse material produzido, totalizando 10 corpos de prova para medição. Vale lembrar que se um defeito desse chegar aos clientes, milhões de reais podem ser perdidos na empresa, evidenciando a grande importância da correta medição e análise estatística.
Nesse sistema os 10 lotes somente serão aprovados se:

1. A média deve estar entre 14,80 cm e 15,20 cm, ou seja, 15±0,20 cm.
2. O desvio padrão não pode ser maior que 0,25 cm.

As medições foram efetuadas e estão arranjadas na tabela a seguir:

Como calculado, a média está dentro dos limites aceitáveis para aprovação do produto, agora iremos realizar o procedimento para obtenção do desvio padrão. A substituição de cada termo pela média será representada na nova tabela para as amostras, observe:

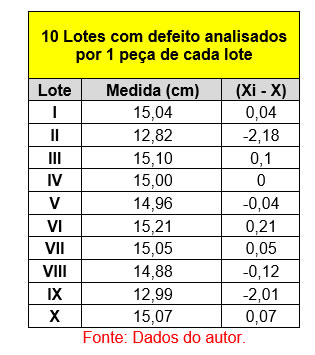
O próximo passo após subtrair a diferença de cada medida com a média é elevar ao quadrado, considerando somente os valores absolutos para os desvios, observe:

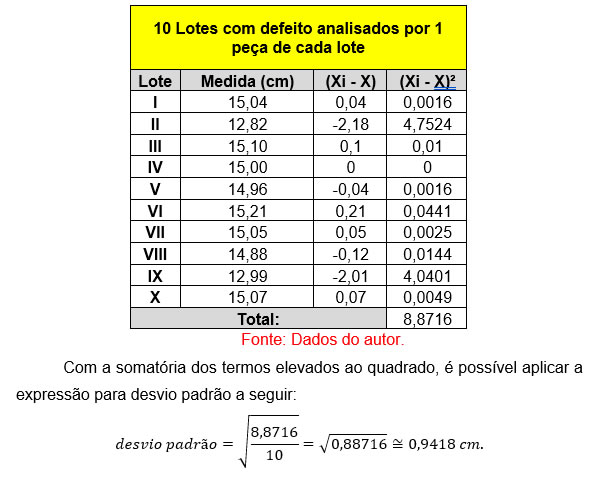
Encontrado o desvio padrão, afirma-se que esse conjunto de 10 lotes apresenta uma média de 15,01 cm, com uma possível variação de ±0,94 cm para cada medida. Assim conclui-se que o material nessa indústria não pode ser disponibilizado para os clientes.