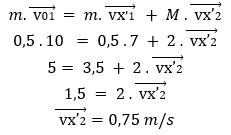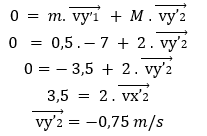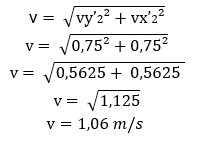CONSERVAÇÃO EM FENÔMENOS NATURAIS – CONSERVAÇÃO DO MOMENTO LINEAR
IFSP - Cursinho Popular
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
Introdução
Tópicos: Conteúdo programático; Momento; Momento Linear; Impulso; Conservação Momento Linear; Colisões; Colisão unidimensional; Colisão bidimensional; Colisões inelásticas; Exercícios.
Conteúdo Programático
1. Momento na Física
2. Momento linear
3. Impulso
4. Teorema do impulso
5. Conservação do momento linear
6. Colisões unidimensionais
7. Colisões bidimensionais
8. Coeficiente de restituição
9. Colisões elásticas
10. Colisões inelásticas
11. Colisões perfeitamente inelásticas
Objetivos deste texto
A partir da leitura deste texto, esperamos que você possa:
I) Conhecer diferentes usos da palavra "momento" no âmbito da Física;
II) Compreender como se calcula o momento linear de um corpo/sistema;
III) Identificar as condições para que ocorra a conservação do momento linear de um sistema;
IV) Compreender como se calcula o impulso exercido sobre um corpo e como ele se relaciona com a variação do momento linear;
V) Diferenciar as características associadas aos diferentes tipos de colisão e de que forma o coeficiente de restituição pode ser utilizado nesse contexto;
VI) Notar a possibilidade de analisar colisões multidimensionais com base nos parâmetros associados a cada um dos eixos cartesianos.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Momento
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
Embora no dia a dia a palavra "momento" costume ser usada para indicar um instante de tempo indeterminado, nas Ciências - especificamente na Física - ela compõe a designação de diversos conceitos, entre eles: momento magnético, momento de dipolo elétrico, momento de uma força, momento de inércia, momento angular e momento linear. Os quatro últimos costumam ser estudados no âmbito da Mecânica. De fato, todos eles estão relacionados com a descrição do movimento de corpos: momento de uma força, momento de inércia e momento angular com
e
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Momento Linear
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
O momento linear de um corpo, também chamado de quantidade de movimento ou quantidade de movimento linear, é definido como:
![]()
Em que "m" é a massa, em quilogramas [kg], "v" é a velocidade, em metros por segundo [m/s] e "p" representa o momento linear, em quilogramas metro por segundo [kg.m/s].
Note que a velocidade e o momento linear contêm uma seta em sua representação. Isso indica que estamos considerando sua natureza vetorial. Em outros contextos (para calcular a energia cinética de um corpo, por exemplo), utilizamos "v" como uma grandeza escalar. Em outras palavras, não era relevante saber qual era a e o da velocidade.Consequentemente, por essa relação vetorial com a velocidade, dizemos que .
Veja um exemplo de cálculo do momento linear.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Impulso
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
Como vimos, o momento linear possui forte relação com a velocidade, sendo diretamente proporcional a ela. Nesse sentido, como a velocidade de um corpo pode ser variável, consequentemente, o momento linear de um corpo também pode variar. Vamos analisar melhor essa questão:
Quando um corpo está em inércia sua velocidade é constante. Logo, a aceleração é nula e, pela segunda lei de Newton (Fr = m.a), a força resultante também será nula. Contudo, quando a velocidade varia, a aceleração não é nula e, como a massa também não pode ser nula, teremos uma força resultante diferente de zero. Usando a segunda lei de Newton e supondo que a massa do corpo é constante, temos que:
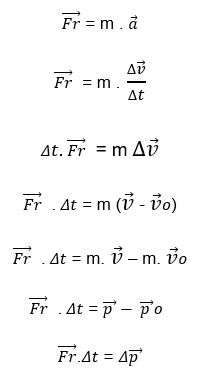
Portanto, a variação de velocidade implica em variação do momento linear (Δp). E, da mesma forma que podemos afirmar que a variação de velocidade é causada por uma força resultante, a variação do momento linear é causada por uma força resultante aplicada por certo intervalo de tempo. O produto de uma força pelo intervalo de tempo de sua aplicação é denominado Impulso:
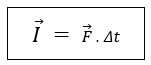
Onde "I" é o Impulso medido em Newton vezes segundo [N.s]. Com isso, podemos reconfigurar nossa afirmação em: A variação do momento linear de um corpo é igual ao Impulso resultante aplicado sobre ele (teorema do Impulso):
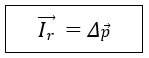
Veja um trecho do Filme "Homem-Aranha", produzido pela "Sony Pictures" em 2002:
Você consegue relacioná-la com os conceitos de Impulso, momento linear e sua variação?
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Conservação do momento linear
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
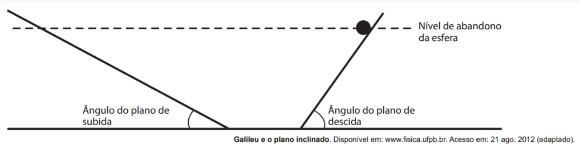
No início dos estudos sobre o momento linear e com o avanço das discussões sobre a mecânica do universo, parecia natural supor que todo objeto que está em movimento - ou que acabou sendo movimentado - diminua sua velocidade até parar. Contudo, pensadores criacionistas como
idealizavam que Deus não iria criar um mecanismo tão imperfeito, ou seja: o universo não poderia cessar seu movimento. Logo, de alguma maneira, "a quantidade do movimento no universo seria constante".
Matematicamente, teríamos:
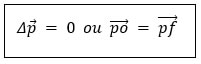
Para desenvolver esse pensamento, podemos imaginar um experimento configurado apenas em uma dimensão (eixo x), da seguinte maneira:
Figura 2 - Configuração I - conservação do momento linear
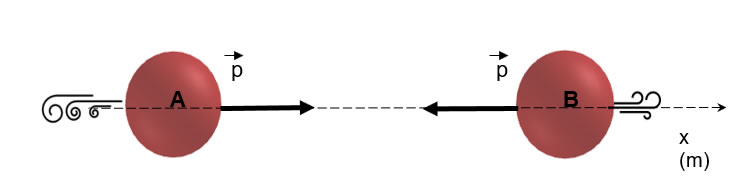
Fonte: Autoria própria
Temos dois corpos pontuais de mesma massa (4 kg) e com módulos de velocidade iguais (2 m/s), porém, em sentidos opostos. Para calcular o momento linear de um sistema basta somar vetorialmente (levando em conta as direções e sentidos) todos os momentos lineares dos corpos que o compõe:
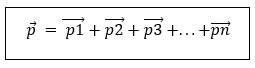
Sendo n o número total de corpos.
Figura 3 - Configuração II - conservação do momento linear
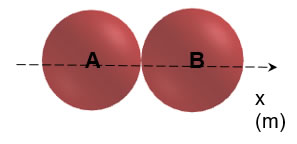
Fonte: Autoria própria
Nessa figura, notamos que depois da colisão frontal, os objetos irão ficar unidos e imóveis. Isso pode ser explicado pelo fato de os vetores de velocidade de cada objeto inicialmente estarem em sentidos opostos, sendo a soma vetorial dos momentos lineares antes da colisão igual a zero. Num segundo, logo após a colisão, temos os objetos unidos e sem movimento, indicando que o momento linear do sistema se conservou. Matematicamente temos:
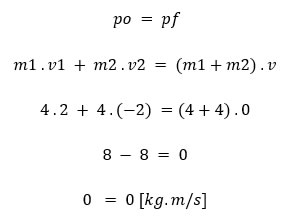
Tome cuidado com o termo "quantidade de movimento" (termo antigo geralmente utilizado para referenciar o momento linear), pois, nesse exemplo percebemos que o sistema pode conter um momento linear nulo mesmo com um movimento perceptível dos corpos, como visto antes da colisão.
Desenvolvendo nossa experiência, agora iremos dobrar a massa de um corpo (ficará sendo 8 kg), configurando-a da seguinte maneira:
Figura 4 - Configuração III conservação do momento linear
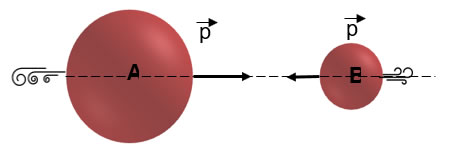
Fonte: Autoria própria
Antes da colisão, teríamos que o momento linear do sistema seria dado por:
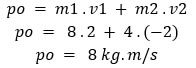
e:
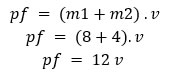
Assumindo que o momento linear do sistema irá se conservar e supondo que após a colisão frontal os corpos permanecem unidos, acoplados um ao outro, podemos escrever que:
![]()
Portanto, após a colisão, os corpos terão uma velocidade residual de 0,67 m/s na direção da velocidade do corpo com o dobro da massa conforme ilustrado na figura a seguir:
Figura 5 - Configuração IV - conservação do momento linear
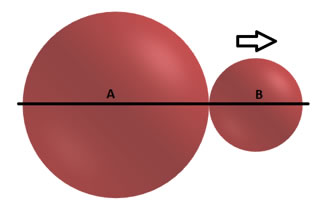
Fonte: Autoria própria
Podemos notar com esses cálculos que não há conservação da velocidade (nem dos corpos, nem do sistema), mas sim, com o fenômeno sendo influenciado pela massa e a velocidade simultaneamente, conservação do momento linear do sistema.
Mas o momento linear de um sistema irá sempre se conservar?
Bem, se lembrarmos do conceito de impulso veremos que não! Na verdade, o momento linear de um sistema só irá se conservar na ausência de forças externas resultantes, ou seja, na ausência de impulsos resultantes. No exemplo anterior da colisão entre os corpos não havia nenhuma força externa resultante. De fato, durante a colisão, o corpo A exerceu uma força no corpo B e o corpo B exerceu uma força no corpo A (de módulos e direções iguais e sentidos contrários conforme a 3ª Lei de Newton). Mas essas são forças internas ao sistema e não forças externas.
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Colisões
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
De forma geral, o estudo de colisões é a área em que o momento linear recebe grande destaque ao possibilitar, a partir de um conjunto de informações, a definição do movimento passado ou a previsão do movimento futuro de um corpo/sistema.
De forma genérica, podemos definir colisão como uma interação, num curto intervalo de tempo, entre dois ou mais corpos que inicialmente encontram-se livres.
Nos estudos sobre momento linear, introduziu o chamado coeficiente de restituição (e), que varia entre zero e um e é calculado da seguinte maneira:
Em que v1 e v2 correspondem às velocidades dos corpos 1 e 2 antes da colisão e v'1 e v'2 representam, respectivamente, as velocidades dos corpos 1 e 2 depois da colisão. Esses valores resultam numa constante física adimensional. Como as colisões duram frações de segundos, seria complexo classificá-las/analisá-las levando em conta características/parâmetros associados ao momento da colisão. Por outro lado, as velocidades dos corpos envolvidos antes e depois da colisão podem ser medidas com certa facilidade, o que evidencia a relevância do coeficiente de restituição como forma de estudo e classificação de colisões. De fato, veja como um mesmo projétil pode se comportar de maneiras diferentes numa colisão.
Tendo em vista o coeficiente de restituição, podemos classificar as colisões em três tipos:
- Colisão elástica (e = 1).
- Colisão inelástica ou parcialmente inelástica (0 < e < 1).
- Colisão perfeitamente inelástica (e = 0)
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Colisão elástica unidimensional
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
Classificamos como elástica a colisão em que há conservação da energia cinética do sistema. Assim, a soma da energia cinética dos corpos antes do encontro deve ter o mesmo valor que a soma da energia cinética dos corpos depois do encontro. Atente-se para uma característica notável da colisão elástica: os corpos envolvidos não se deformam (não se amassam, não se contraem), o que faz sentido ao lembramos que para emitir uma onda ou deslocar matéria é necessário utilizar energia. Portanto, numa colisão elástica, a energia mecânica não é transformada em outros tipos de energia (sonora, térmica etc.). Trata-se de um tipo de colisão praticamente inexistente no dia a dia, uma vez que implica numa colisão em que não há emissão de som, por exemplo.
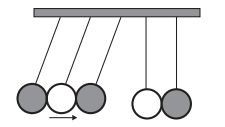
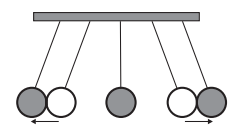
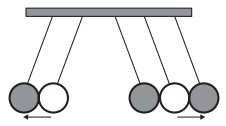
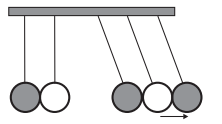
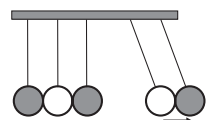
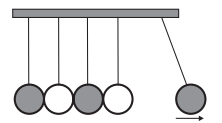
Figura 6 - Pêndulo de Newton
Fonte: GIPHY (http://gph.is/15y3q0Z)
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Colisão Bidimensional (2D)
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
A conservação do momento linear é sempre válida, independentemente de se tratar de colisão uni, bi ou tridimensional. Contudo, nos casos bidimensional e tridimensional, os cálculos devem ser feitos de maneira individualizada em cada eixo (x, y e z). Nesse sentido, para casos bidimensionais teremos a inclusão de relações trigonométricas como seno e cosseno nos cálculos (para decompor os vetores). Vejamos um exemplo:
Um corpo em movimento bidimensional contém momento linear de 200 kg.m/s orientado num ângulo de 30º em relação ao eixo x. Determine seu momento linear no eixo x e seu momento linear no eixo Y:
Figura 7 - Representação do momento linear de um corpo se movendo em duas dimensões
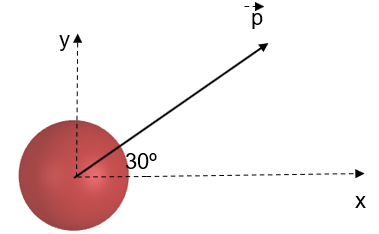
Fonte: Autoria própria
Resolução:
Observe que a hipotenusa do triângulo retângulo corresponde ao momento linear resultante. Os catetos desse triângulo correspondem às componentes do momento linear nos eixos x e y:

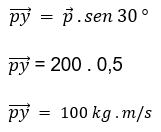
Vale lembrar que o vetor velocidade está sempre na mesma direção e sentido do vetor do momento linear. Assim, poderíamos calcular px e py como:
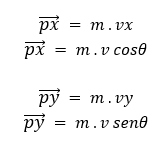
Caso quiséssemos calcular o momento linear resultante a partir de suas componentes teríamos que recorrer ao chamado Teorema de Pitágoras: num triângulo retângulo, a soma dos catetos ao quadrado equivale à hipotenusa ao quadrado. No caso analisado a cima, teríamos que:
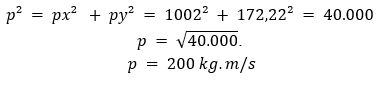 .
.
Em síntese: para a análise de colisões bidimensionais devemos analisar separadamente os vetores em cada eixo:
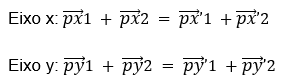
Ou:
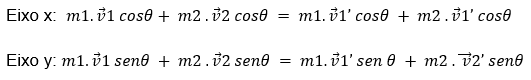
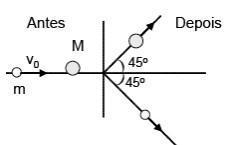
Figura 8 - Colisão Bidimensional I
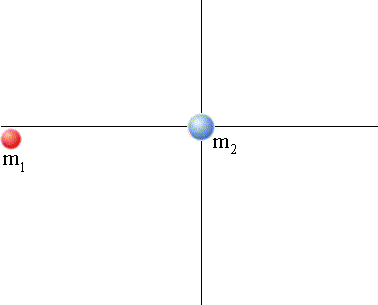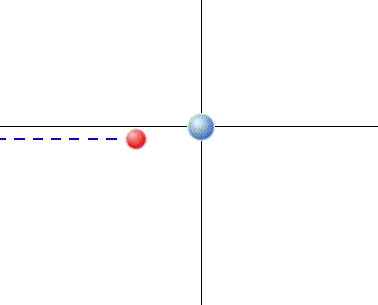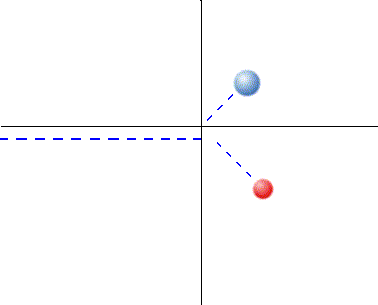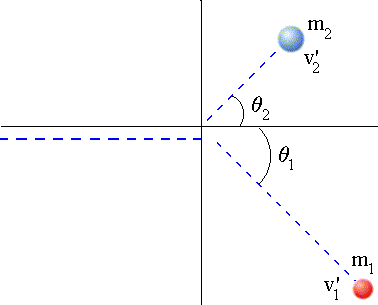
Fonte: Oliveira, Mizukoshi (https://propg.ufabc.edu.br/mnpef-sites/leis-de-conservacao/colisoes/)
Para o exemplo da Figura 8 a análise do momento linear ficaria como:
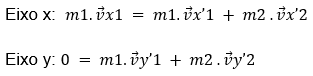
Duas observações para esse exemplo: i) antes da colisão, apenas o corpo 1 possui momento linear, já que a velocidade do segundo corpo é igual a zero; ii) antes do impacto, não há momento linear no eixo y, uma vez que o corpo 1 se move apenas no eixo x.
Figura 9 - Colisões num jogo de bilhar
Fonte: Sporza (https://gph.is/g/Zywv0Mb)
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
COLISÕES INELÁSTICAS
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
Ao contrário do que ocorre nas colisões elásticas, nas colisões inelásticas não ocorre conservação da energia mecânica: ela é transformada em outros tipos de energia (térmica, sonora etc.). Por exemplo: na Figura 11, a energia cinética associada aos carros foi transformada em energias como a energia sonora (do impacto e dos pneus).
Figura 11 - Colisão inelástica

Fonte: Oliveira, Mizukoshi (https://propg.ufabc.edu.br/mnpef-sites/leis-de-conservacao/colisoes/)
COLISÕES PERFEITAMENTE INELÁSTICAS
Numa colisão perfeitamente inelástica, os corpos ficam unidos após a colisão – conforme exemplificado na Figura 12. Para esse tipo de evento, o coeficiente de restituição é igual a zero (e = 0) e, novamente, não ocorre conservação da energia mecânica. De fato, este é o tipo de colisão em que há maior perda de energia mecânica.
Figura 12 - Colisão perfeitamente inelástica
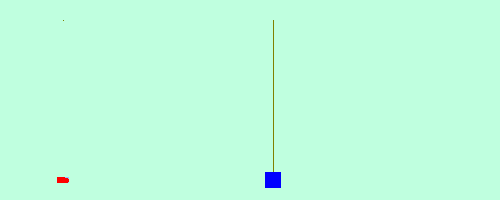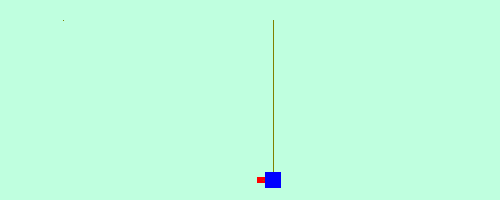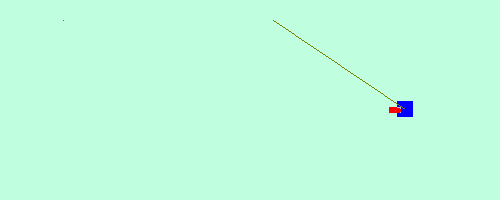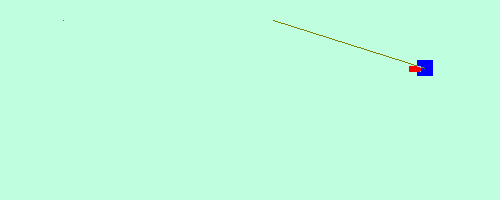
Fonte: Oliveira, Mizukoshi (https://propg.ufabc.edu.br/mnpef-sites/leis-de-conservacao/colisoes/)
Por fim, vale frisar três pontos fundamentais:
I) A análise de colisões inelásticas e perfeitamente inelásticas em duas ou três dimensões também envolverá a decomposição do vetor momento linear em cada eixo.
II) Embora raramente a energia mecânica se conserve no contexto de colisões (apenas nas colisões elásticas, que são raríssimas), a lei de conservação do momento linear vale para todos os tipos de colisões.
III) A conservação do momento linear não é válida apenas no caso de colisões, mas também no caso de outros tipos de interação entre corpos (quando um canhão/revólver dispara uma bala, quando uma pessoa sobre uma canoa salta para um mergulho etc.).
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
Questões de vestibulares
Como citar este documento: SILVA, André Coelho da; LIMA, Jonas da Silva Gomes de; ALMEIDA FILHO, Luiz Antonio de. Conservação em fenômenos naturais – Conservação do momento linear. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/conservacao-momento-linear.html. Acesso em: [data de acesso].
1) (ENEM 2017)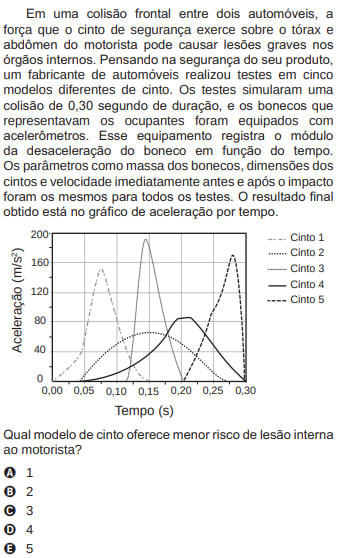
2) (FUVEST 2019 - Segunda fase) 
3) (FUVEST - 2015 - Segunda Fase - Modificada)

4) (FUVEST - 2015)

5) (FUVEST - 2015)

6) (FUVEST - 2013)
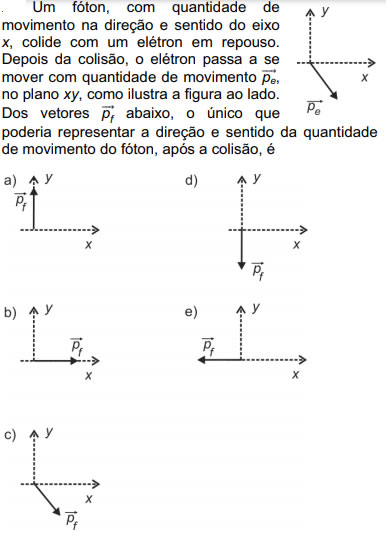
7) (FUVEST - 2013 - Segunda Fase)

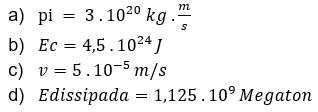
8) (Fuvest - 2013)

9) (FUVEST - 2012)
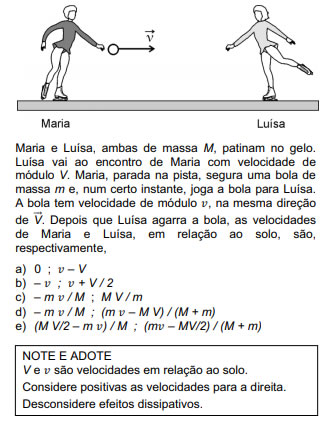
10) (FUVEST - 2012)

11) (Unicamp - 2012)
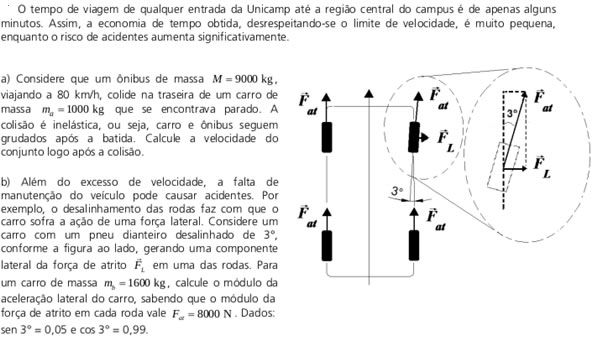
12) (Unicamp - 2016)

13) (UNESP- 2013)
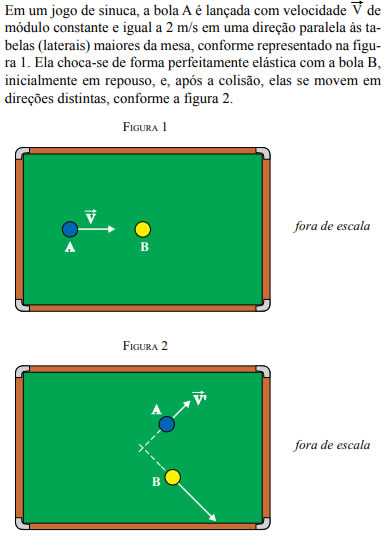

14) (UNESP - 2018)
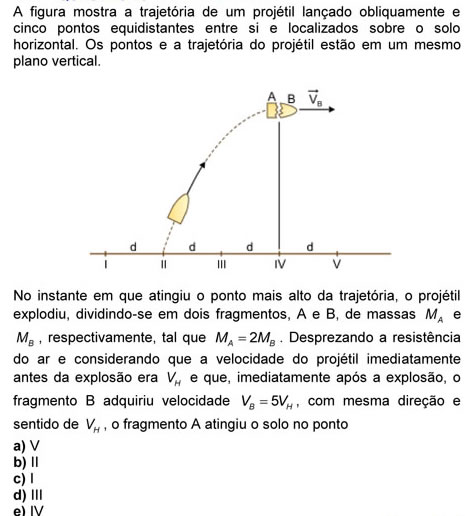
15) (UNESP - 2015)
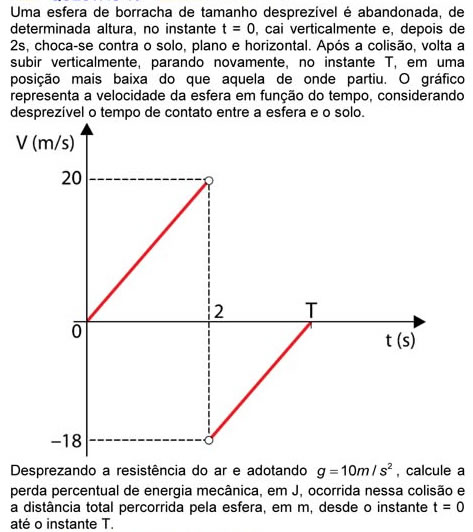
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021
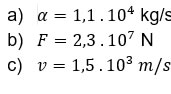


 3.m.v = M.V
3.m.v = M.V