Contextualização

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Você é adepto da prática de atividades físicas? Se sim, com certeza já ouviu falar da importância da amplitude para a execução correta de um movimento. Um tenista, por exemplo, precisa da amplitude correta em seus movimentos para acertar a bola e marcar o ponto, concorda? E isso tem tudo a ver com o assunto que iremos estudar adiante: ângulos!

Para efeito de melhor ilustração, outro exemplo da importância dos ângulos, também presente nos esportes, é o que acontece com os arremessadores de peso. Eles treinam para aperfeiçoar a sua técnica de lançamento de modo a conseguirem arremessar o objeto o mais longe possível, e isso acontece quando atingem, em seu arremesso, o ângulo de 45º em relação ao solo.

Após essa breve contextualização, podemos começar a estudar os ângulos, entes geométricos que constituem um assunto elementar da Geometria Plana. Veremos os principais conceitos e resolveremos exercícios para a fixação do conteúdo. Ao final, vocês encontrarão exercícios propostos para avaliar os conhecimentos adquiridos.

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Ângulo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

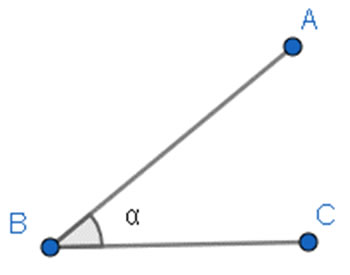
Podemos pensar em um ângulo como a abertura compreendida entre duas semirretas distintas e de mesma origem.

Temos que o ponto B (ponto em comum entre as duas semirretas) é o vértice do ângulo e as semirretas    são os lados do ângulo

Indicamos o ângulo em questão como:  

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Medida de um ângulo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Medir um ângulo significa compará-lo com um arco unitário pré-estabelecido. Nessa primeira parte de nosso estudo usaremos o grau, bem como seus submúltiplos, como parâmetro para medir nossos ângulos.

Grau(º): é o arco unitário que corresponde a da circunferência

 

Figura 4 - Arco de 1º

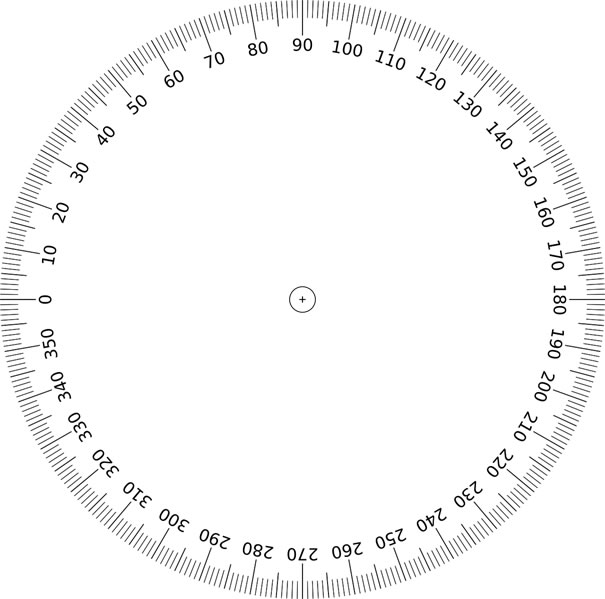
Fonte: Pixabay (2021) (https://pixabay.com/pt/vectors/c%c3%adrculo-matem%c3%a1tica-educa%c3%a7%c3%a3o-360-41073/)

 

Portanto, se pensarmos em um ângulo de , como no exemplo do arremesso de peso, estamos pensando em uma abertura quarenta e cinco vezes maior que   da circunferência

Figura 5 - Ângulo de 45º

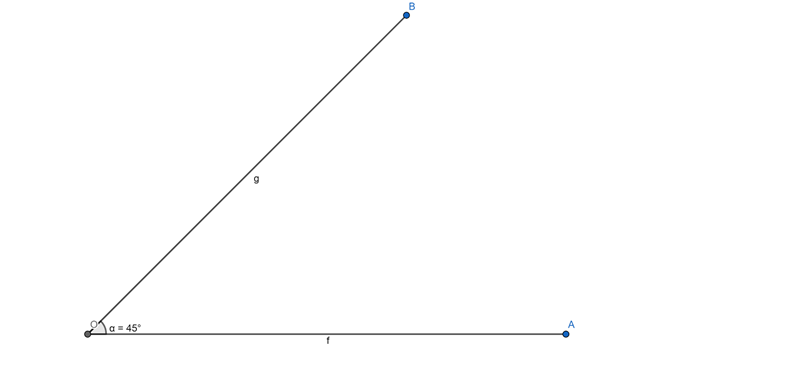
Fonte: Matheus Soares (2020)

Indicamos a medida do ângulo em questão como:

Também é bastante comum indicar a medida de um ângulo utilizando as letras gregas minúsculas, por exemplo,

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Bissetriz de um ângulo

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

A bissetriz de um ângulo é a semirreta com origem no vértice desse ângulo e que o divide em dois ângulos congruentes, ou seja, dois ângulos que possuem a mesma medida.

Figura 6 - Bissetriz de um ângulo

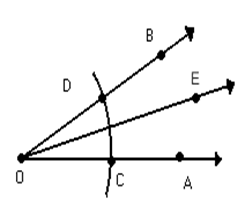
Fonte: Fábio Mascai (2020)

Na figura, a semirreta   é a bissetriz do ângulo   , pois ela o divide em dois ângulos congruentes: 

Temos que: 

Exemplo 1: Calcular x, sabendo que a semirreta   é bissetriz do ângulo   .

Figura 7 - Exemplo 1

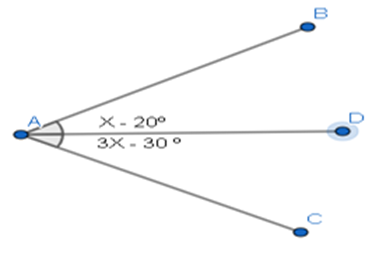
Fonte: Fábio Mascai (2020)

       

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Classificação dos ângulos

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

• Ângulo Reto: É todo ângulo que tem medida igual a 

Figura 8 - Ângulo reto

Fonte: Fábio Mascai (2020)

• Ângulo Agudo: É todo ângulo cuja medida é menor que a de um ângulo reto
  
  

  Figura 9 - Ângulo agudo

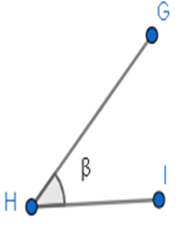
Fonte: Fábio Mascai (2020)

Se pensar pensarmos na medida   de um ângulo agudo qualquer, temos que: 

• Ângulo Obtuso: É todo ângulo cuja medida é maior que a de um ângulo reto
  
  

  Figura 10 - Ângulo obtuso
  
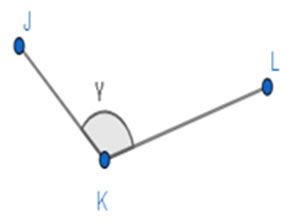
  Fonte: Fábio Mascai (2020)

  Se pensarmos na medida   de um ângulo obtuso qualquer, temos que: 
  
  
  
  
  
  

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Ângulos complementares

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Dois ângulos cujas medidas somam   são chamados ângulos complementares.

Figura 11 - Ângulos complementares

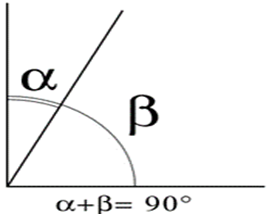
Fonte: Fábio Mascai (2020)

Exemplo 2: Calcule x, sendo     .

Figura 12 – Exemplo 2

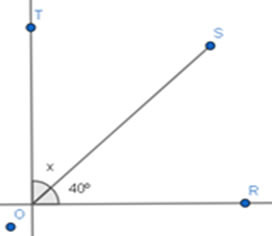
Fonte: Fábio Mascai (2020)

   


Exemplo 3: Sendo   , determine o valor de cada ângulo.

Figura 13 - Exemplo 3

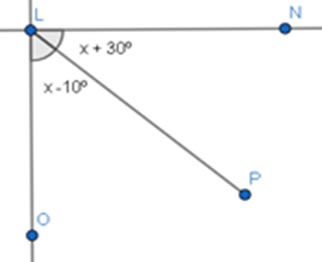
Fonte: Fabio Mascai (2020)

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Ângulos suplementares

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Dois ângulos cujas medidas somam   são chamados ângulos suplementares.

Figura 14 - Ângulos suplementares

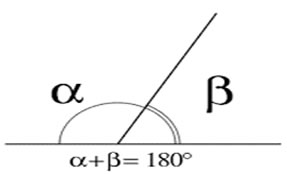
Fonte: Fábio Mascai (2020)

Exemplo 4: Na figura abaixo, calcule o valor de x.

Figura 15 - Exemplo 4

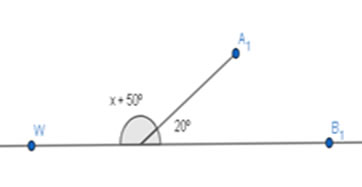
Fonte: Fábio Mascai (2020)

Os ângulos em questão são suplementares,portanto:

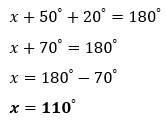
Obs:vale lembrar que x não é o valor de nenhum dos dois ângulos

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Ângulos opostos pelo vértice (O.P.V.)

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Duas retas concorrentes determinam pares de ângulos opostos pelo vértice.

Figura 16 - Ângulos O.P.V.

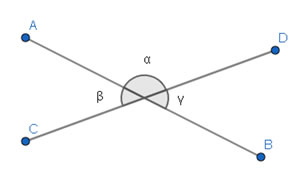
Fonte: Fábio Mascai (2020)

Propriedade: dois ângulos opostos pelo vértice são sempre congruentes.

Demonstração:



Exemplo 5: Com os dados da figura, calcule o valor de 



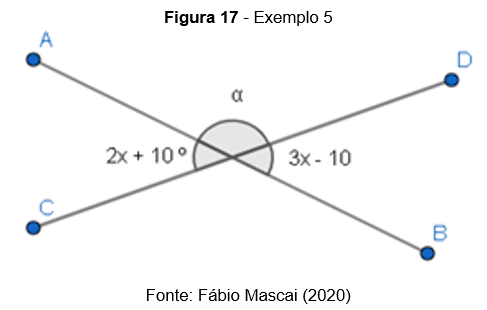
Os ângulos indicados por são opostos pelo vértice:


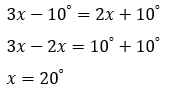
O ângulo de medida α é suplementar a ambos os outros dois ângulos,portanto:

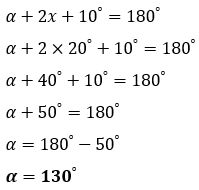
Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Paralelismo e suas consequências

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

Quando temos duas retas paralelas cortadas por uma transversal, elas determinam pares de ângulos importantes para o nosso estudo.

Figura 18 - Retas paralelas cortadas por uma transversal

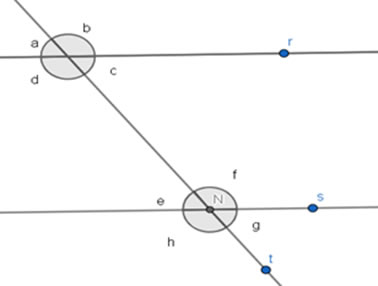
Fonte: Fábio Mascai (2020)

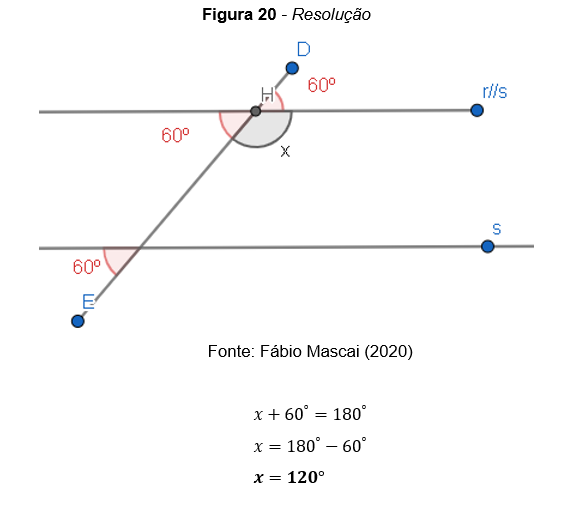
Exemplo 6: Determine o valor de x na figura seguinte


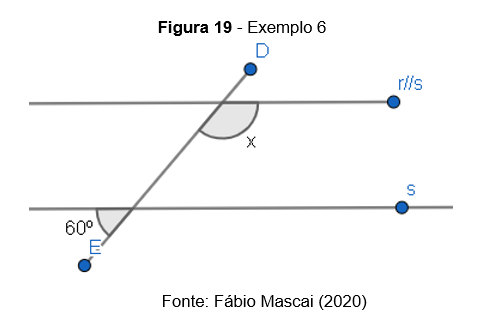
Temos que:

Exemplo 7: Calcule o valor de x

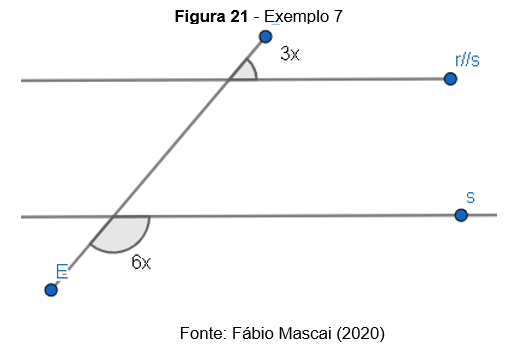
Os ângulos em questão são colaterais externos e,portanto,são suplementares



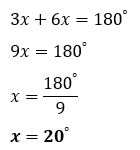
Obs:vale lembrar que x não é o valor de nenhum dos dois ângulos

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021

Exercícios

Como citar este documento: CRUZ, Paulo Henrique Correia Araújo da; CAMPOS, Ayumi de Kato; SOARES, Matheus Ferreira; MASCAI, Fábio Amaral Augusto. Ângulos. Cursinho Popular IFSP Itapetininga, Itapetininga, fev. 2021. Disponível em: https://cursinhopopular.itp.ifsp.edu.br/site/cursinho/home/materias/angulos.html. Acesso em: [data de acesso].

P1. Calcule o valor de y

1. 

2. 

3. 

4. 

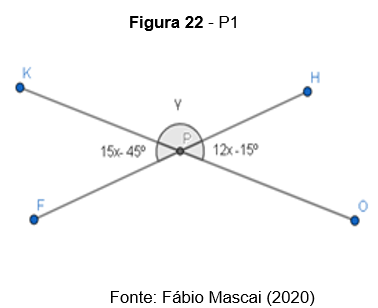
P2. Calcule o valor de x na figura, sendo   

1. 

2. 

3. 

4. 

5. 

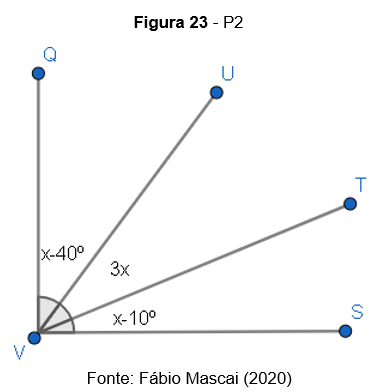
P3. (Modelo Enem) São dados dois ângulos adjacentes em que a medida de um é o triplo da medida do outro e a medida do complemento do ângulo entre as suas bissetrizes é 50°. A medida do complemento da soma ângulos dados é igual a:

1. 

2. 

3. 

4. 

5. 

 

P4. A medida de um ângulo x é igual a metade da medida de seu complemento. O complemento de x mede:

1. 

2. 

3. 

4. 

5. 

P5. (ENEM) A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais

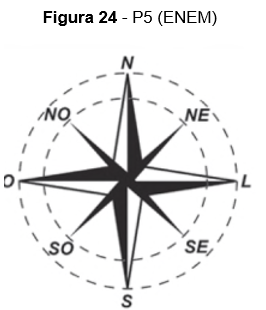
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:

• 1ª mudança: 135° no sentido anti-horário;

• 2ª mudança: 60° no sentido horário;

• 3ª mudança: 45° no sentido anti-horário.

Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.

Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?

1.  no sentido horário

2.  no sentido anti-horário

3.  no sentido anti-horário

4.  no sentido anti-horário

5.  no sentido horário

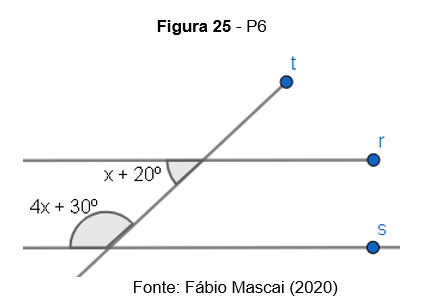
P6. As retas r e s são interceptadas pela transversal t, conforme a figura. O valor de x para que r e s sejam paralelas é:

1. 

2. 

3. 

4. 

5. 

P7. (Modelo ENEM) Duas ruas paralelas no condomino Rio Encantado são cortadas transversalmente por outra rua que forma com as primeiras angulos colaterias internos de tal modo que um excede o outro em 30°. O maior desses ângulos mede:

1. 

2. 

3. 

4. 

5. 

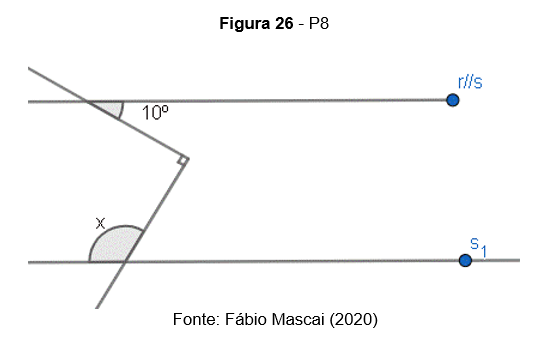
P8. Na figura, r e s são paralelas, então x vale:

1. 

2. 

3. 

4. 

5. 

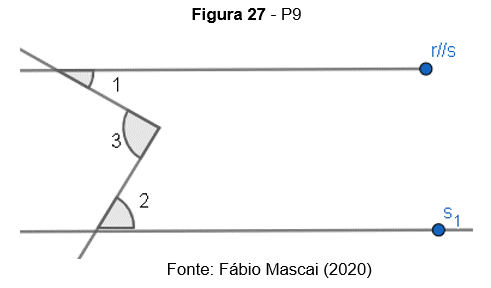
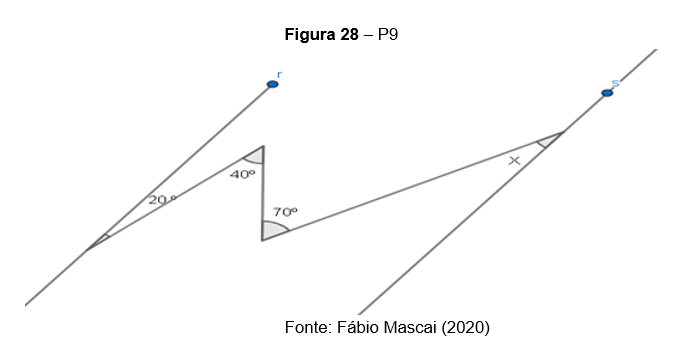
P9. (Modelo ENEM)  Na figura, as retas r e s são paralelas, o ângulo 1 mede 45° e o ângulo 2 mede 55°. A medida, em graus, do ângulo 3 é:

1. 

2. 

3. 

4. 

5. 

P10. Calcule o valor de x, sendo r e s paralelas:

1. 

2. 

3. 

4. 

5. 

 

Licenciada sob uma licença Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. Cursinho Popular IFSP Itapetininga 2021